题目内容
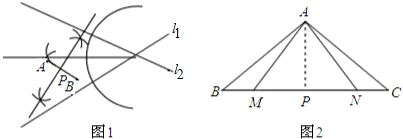
（1）如图1，求作一点P，使P到两条直线的距离相等，且使PA=PB；（保留作图痕迹）
（2）如图2，在△ABC中，AB=AC，点M、N在边BC上，且AM=AN，试判断BM和CN的大小关系，并说明理由．
解：①
②BM=CN．
过点A作AP⊥BC于P，
∵AB=AC，AP⊥BC，
∴BP=CP，
又∵AM=AN，AP⊥MN，
∴PM=PN，
∴BP-MP=CP-NP．
即BM=CN．
分析：①连接AB，分别作角平分线和中垂线，交点P即可；
②过点A作AP⊥BC于P，根据等腰三角形的性质，高、中线、角平分线三线合一，求证BP=CP，PM=PN即可证明．
点评：此题主要考查学生对角平分线的性质、线段垂直平分线的性质和等腰三角形的性质的理解和掌握，此题涉及到的知识点较多，属于中档题．
②BM=CN．
过点A作AP⊥BC于P，
∵AB=AC，AP⊥BC，
∴BP=CP，
又∵AM=AN，AP⊥MN，
∴PM=PN，
∴BP-MP=CP-NP．
即BM=CN．
分析：①连接AB，分别作角平分线和中垂线，交点P即可；
②过点A作AP⊥BC于P，根据等腰三角形的性质，高、中线、角平分线三线合一，求证BP=CP，PM=PN即可证明．
点评：此题主要考查学生对角平分线的性质、线段垂直平分线的性质和等腰三角形的性质的理解和掌握，此题涉及到的知识点较多，属于中档题．
练习册系列答案
发散思维新课堂系列答案
相关题目
