题目内容
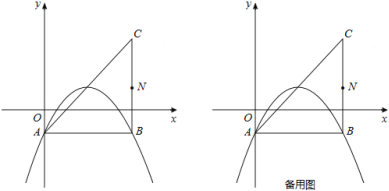
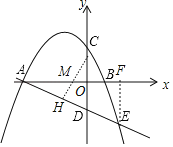
【题目】如图,已知二次函数y=ax2+4ax+c(a≠0)的图象交x轴于A、B两点(A在B的左侧),交y轴于点C.一次函数y=﹣![]() x+b的图象经过点A,与y轴交于点D(0,﹣3),与这个二次函数的图象的另一个交点为E,且AD:DE=3:2.
x+b的图象经过点A,与y轴交于点D(0,﹣3),与这个二次函数的图象的另一个交点为E,且AD:DE=3:2.
(1)求这个二次函数的表达式;
(2)若点M为x轴上一点,求MD+![]() MA的最小值.
MA的最小值.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先把D点坐标代入y=﹣![]() x+b中求得b,则一次函数解析式为y=﹣
x+b中求得b,则一次函数解析式为y=﹣![]() x﹣3,于是可确定A(﹣6,0),作EF⊥x轴于F,如图,利用平行线分线段成比例求出OF=4,接着利用一次函数解析式确定E点坐标为(4,﹣5),然后利用待定系数法求抛物线解析式;
x﹣3,于是可确定A(﹣6,0),作EF⊥x轴于F,如图,利用平行线分线段成比例求出OF=4,接着利用一次函数解析式确定E点坐标为(4,﹣5),然后利用待定系数法求抛物线解析式;
(2)作MH⊥AD于H,作D点关于x轴的对称点D′,如图,则D′(0,3),利用勾股定理得到AD=3![]() ,再证明Rt△AMH∽Rt△ADO,利用相似比得到MH=
,再证明Rt△AMH∽Rt△ADO,利用相似比得到MH=![]() AM,加上MD=MD′,MD+
AM,加上MD=MD′,MD+![]() MA=MD′+MH,利用两点之间线段最短得到当点M、H、D′共线时,MD+
MA=MD′+MH,利用两点之间线段最短得到当点M、H、D′共线时,MD+![]() MA的值最小,然后证明Rt△DHD′∽Rt△DOA,利用相似比求出D′H即可.
MA的值最小,然后证明Rt△DHD′∽Rt△DOA,利用相似比求出D′H即可.
解:(1)把D(0,﹣3)代入y=﹣![]() x+b得b=﹣3,
x+b得b=﹣3,
∴一次函数解析式为y=﹣![]() x﹣3,
x﹣3,
当y=0时,﹣![]() x﹣3=0,解得x=﹣6,则A(﹣6,0),
x﹣3=0,解得x=﹣6,则A(﹣6,0),
作EF⊥x轴于F,如图,
∵OD∥EF,
∴![]() =
=![]() =
=![]() ,
,
∴OF=![]() OA=4,
OA=4,
∴E点的横坐标为4,
当x=4时,y=﹣![]() x﹣3=﹣5,
x﹣3=﹣5,
∴E点坐标为(4,﹣5),
把A(﹣6,0),E(4,﹣5)代入y=ax2+4ax+c得![]() ,解得
,解得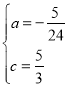 ,
,
∴抛物线解析式为![]() ;
;
(2)作MH⊥AD于H,作D点关于x轴的对称点D′,如图,则D′(0,3),
在Rt△OAD中,AD=![]() =3
=3![]() ,
,
∵∠MAH=∠DAO,
∴Rt△AMH∽Rt△ADO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MH=![]() AM,
AM,
∵MD=MD′,
∴MD+![]() MA=MD′+MH,
MA=MD′+MH,
当点M、H、D′共线时,MD+![]() MA=MD′+MH=D′H,此时MD+
MA=MD′+MH=D′H,此时MD+![]() MA的值最小,
MA的值最小,
∵∠D′DH=∠ADO,
∴Rt△DHD′∽Rt△DOA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得D′H=
,解得D′H=![]() ,
,
∴MD+![]() MA的最小值为
MA的最小值为![]() .
.

【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)根据上述信息可知:甲命中环数的中位数是_____环,乙命中环数的众数是______环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)