题目内容
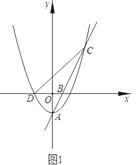
【题目】如图1,抛物线![]() 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
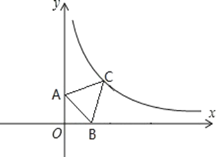
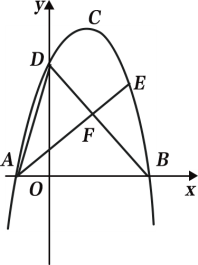
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
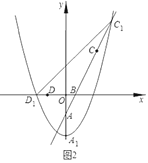
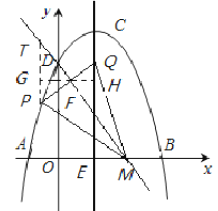
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.


【答案】(1)![]() ;(2)E(2,3)或(1,4);(3)P点横坐标为
;(2)E(2,3)或(1,4);(3)P点横坐标为![]()
【解析】
(1) 抛物线![]() 的顶点为C(1,4),设抛物线的解析式为
的顶点为C(1,4),设抛物线的解析式为![]() ,由抛物线过点B,(3,0),即可求出a的值,即可求得解析式;
,由抛物线过点B,(3,0),即可求出a的值,即可求得解析式;
(2)过点E、F分别作x轴的垂线,交x轴于点M、N,设点E的坐标为![]() ,求出A、D点的坐标,得到OM=x,则AM=x+1,由AF=2EF得到
,求出A、D点的坐标,得到OM=x,则AM=x+1,由AF=2EF得到![]() ,从而推出点F的坐标
,从而推出点F的坐标![]() ,由
,由![]() ,列出关于x的方程求解即可;
,列出关于x的方程求解即可;
(3)先根据待定系数法求出直线DM的解析式为y=-2x+3,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H.证明△FGP≌△FHQ,得到FG=FH,PT=![]() GH.设点P(m,-m+2m+3),则T(m,-2m+3),则PT=m-4m,GH=1-m,可得m-4m=
GH.设点P(m,-m+2m+3),则T(m,-2m+3),则PT=m-4m,GH=1-m,可得m-4m=![]() (1-m),解方程即可.
(1-m),解方程即可.
(1)∵抛物线的顶点为C(1,4),
∴设抛物线的解析式为![]() ,
,
∵抛物线过点B,(3,0),
∴![]() ,
,
解得a=-1,
∴设抛物线的解析式为![]() ,
,
即![]() ;
;
(2)如图,过点E、F分别作x轴的垂线,交x轴于点M、N,设点E的坐标为![]() ,
,

∵抛物线的解析式为![]() ,
,
当y=0时, 解得x=-1或x=3, ∴A(-1.0), ∴点D(0,3), ∴过点BD的直线解析式为 则OM=x,AM=x+1, ∴ ∴ ∴ ∴ 解得x=1或x=2, ∴点E的坐标为(2,3)或(1,4); (3)设直线DM的解析式为y=kx+b,过点D(0,3),M( 可得, 解得k=-2,b=3, ∴直线DM的解析式为y=-2x+3, ∴ ∴tan∠DMO=2, 如图,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H. ∵PQ⊥MT, ∴∠TFG=∠TPF, ∴TG=2GF,GF=2PG, ∴PT= ∵PF=QF, ∴△FGP≌△FHQ, ∴FG=FH, ∴PT= 设点P(m,-m+2m+3),则T(m,-2m+3), ∴PT=m-4m,GH=1-m, ∴m-4m= 解得: ∴点P的横坐标为![]() ,
,![]() ,点F在直线BD上,
,点F在直线BD上,![]() ,
,![]() ,
,![]() ,
,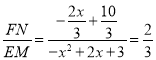 ,
,![]() ,0),
,0),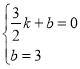 ,
,![]() ,
,![]() ,
,
![]() GF,
GF,![]() GH.
GH.![]() (1-m),
(1-m),![]() ,或
,或![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案