题目内容
在Rt△ABC中,∠C=90°,BC=3,AC=4,点D在斜边AB上,且满足DC2=DA·DB;则DB=
1.8或2.5.
试题分析:由勾股定理可得:AB=5;如图①,当CD⊥AB时,则有△BCD∽△CAD,所以
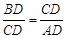 ,即CD2=AD·CD,由三角形面积公式求得CD=3×4÷5=2.4,在Rt△BCD中,由勾股定理可知
,即CD2=AD·CD,由三角形面积公式求得CD=3×4÷5=2.4,在Rt△BCD中,由勾股定理可知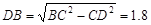 ;如图②,当D是斜边AB的中点时,则有AD=BD=CD,所以CD2=AD·BD,此时,DB=2.5.所以DB的长度是1.8或2.5.
;如图②,当D是斜边AB的中点时,则有AD=BD=CD,所以CD2=AD·BD,此时,DB=2.5.所以DB的长度是1.8或2.5.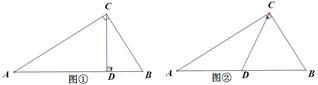

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
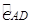 上一点(不与点C、A、D重合),连接BP与CD交于点G.
上一点(不与点C、A、D重合),连接BP与CD交于点G. 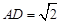 ,
,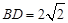 ,求AB的值.
,求AB的值.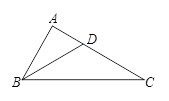

 的值 .
的值 .
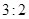 B.
B.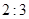 C.
C.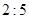 D.
D.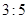
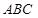 中,
中,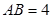 ,当直角三角板
,当直角三角板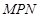 的
的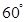 角的顶点
角的顶点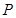 在
在 上移动时,斜边
上移动时,斜边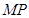 始终经过
始终经过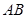 边的中点
边的中点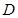 ,设直角三角板的另一直角边
,设直角三角板的另一直角边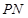 与
与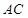 相交于点E.设
相交于点E.设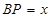 ,
,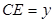 ,那么
,那么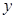 与
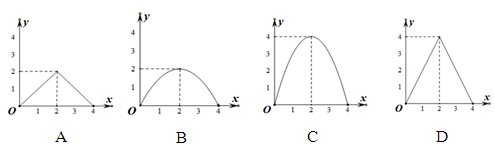
与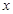 之间的函数图象大致是( )
之间的函数图象大致是( )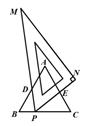
 ,那么
,那么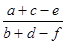 = .
= .