题目内容
如图1,在平面直角坐标系中,已知点M的坐标是(3,0),半径为2的⊙M交x轴于E、F两点,过点P(-1,0)作⊙M的切线,切点为点A,过点A作AB⊥x轴于点C,交⊙M于点B.抛物线y=ax2+bx+c经过P、B、M三点.(1)求该抛物线的函数表达式;
(2)若点Q是抛物线上一动点,且位于P、B两点之间,设四边形APQB的面积为S,点Q的横坐标为x,求S与x之间的函数关系式,并求S的最大值和此时点Q的坐标;
(3)如图2,将弧AEB沿弦AB对折后得到弧AE′B,试判断直线AF与弧AE′B的位置关系,并说明理由.

【答案】分析:(1)连接AM,则AM⊥PA,又AB⊥x轴,可知∠MAC=∠APM,Rt△APM中,sin∠APM=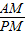 =
=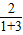 =
= ,故∠APM=30°,在Rt△ACM中,AM=2,∠MAC=∠APM=30°,解直角三角形可求CM,AC,确定A点坐标,根据对称性求B点坐标,抛物线过P、M,设抛物线交点式,将B点坐标代入即可;
,故∠APM=30°,在Rt△ACM中,AM=2,∠MAC=∠APM=30°,解直角三角形可求CM,AC,确定A点坐标,根据对称性求B点坐标,抛物线过P、M,设抛物线交点式,将B点坐标代入即可;
(2)如图1,过Q点作QH⊥x轴,垂足为H,根据S四边形APQB=S△APC+S△PQH+S梯形BCHQ表示面积,利用函数的性质求面积最大值及此时Q点的坐标;
(3)相切.如图2,连接AE,证明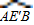 的圆心为E点,判断∠EAF=90°即可.
的圆心为E点,判断∠EAF=90°即可.
解答:解:(1)连接AM,∵PA切⊙M于点A,
∴AM⊥PA,又AB⊥x轴,
∴∠MAC=∠APM,Rt△APM中,PM=PO+OM=1+3=4,AM=2,
∴sin∠APM=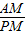 =
= ,∠APM=30°,
,∠APM=30°,
在Rt△ACM中,AM=2,∠MAC=∠APM=30°,
CM=AM•sin30°=2× =1,AC=AM•cos30°=2×
=1,AC=AM•cos30°=2×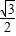 =
=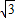 ,
,
∴OC=OM-CM=3-1=2,A(2,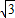 ),
),
∵A、B两点关于x轴对称,
∴B(2,-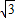 ),
),
∵抛物线过P(-1,0)、M(3,0),设抛物线解析式为y=a(x+1)(x-3),
将B(2,-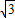 )代入,得a(2+1)(2-3)=-
)代入,得a(2+1)(2-3)=-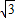 ,解得a=
,解得a=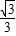 ,
,
∴y=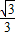 (x+1)(x-3)=
(x+1)(x-3)=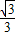 x2-
x2-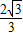 x-
x-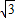 ;
;
(2)如图1,过Q点作QH⊥x轴,垂足为H,由(1)得H(x,0),Q(x,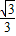 x2-
x2-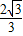 x-
x-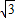 )
)
S四边形APQB=S△APC+S△PQH+S梯形BCHQ= ×PC×AC+
×PC×AC+ ×PH×QH+
×PH×QH+ ×(QH+BC)×CH
×(QH+BC)×CH
= ×3×
×3×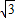 +
+ ×(x+1)×(-
×(x+1)×(-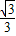 x2+
x2+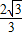 x+
x+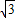 )+
)+ ×(
×(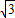 -
-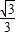 x2+
x2+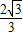 x+
x+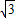 )×(2-x)
)×(2-x)
=-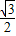 x2+
x2+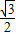 x+4
x+4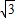 ,
,
∵-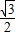 <0,四边形APQB的面积有最大值,
<0,四边形APQB的面积有最大值,
当x= 时,四边形APQB的面积最大值为
时,四边形APQB的面积最大值为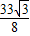 ,此时Q(
,此时Q( ,-
,-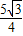 );
);
(3)直线AF与弧AE′B相切.如图2,连接AE,
由(1)可知,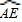 度数为60°,根据对称性可知
度数为60°,根据对称性可知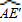 度数为60°,△AEE′为等边三角形,
度数为60°,△AEE′为等边三角形,
∴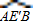 的圆心为E点,∠EAF=∠EAC+∠CAF=30°+60°=90°,
的圆心为E点,∠EAF=∠EAC+∠CAF=30°+60°=90°,
∴直线AF与弧AE′B相切.
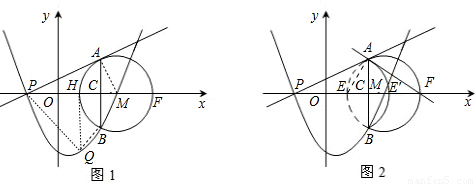
点评:本题考查了二次函数解析式的确定、图形面积的求法、圆心角定理、切线的性质与判定、特殊三角形的判定和性质等知识点.
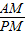 =
=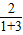 =
= ,故∠APM=30°,在Rt△ACM中,AM=2,∠MAC=∠APM=30°,解直角三角形可求CM,AC,确定A点坐标,根据对称性求B点坐标,抛物线过P、M,设抛物线交点式,将B点坐标代入即可;
,故∠APM=30°,在Rt△ACM中,AM=2,∠MAC=∠APM=30°,解直角三角形可求CM,AC,确定A点坐标,根据对称性求B点坐标,抛物线过P、M,设抛物线交点式,将B点坐标代入即可;(2)如图1,过Q点作QH⊥x轴,垂足为H,根据S四边形APQB=S△APC+S△PQH+S梯形BCHQ表示面积,利用函数的性质求面积最大值及此时Q点的坐标;
(3)相切.如图2,连接AE,证明
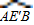 的圆心为E点,判断∠EAF=90°即可.
的圆心为E点,判断∠EAF=90°即可.解答:解:(1)连接AM,∵PA切⊙M于点A,
∴AM⊥PA,又AB⊥x轴,
∴∠MAC=∠APM,Rt△APM中,PM=PO+OM=1+3=4,AM=2,
∴sin∠APM=
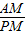 =
= ,∠APM=30°,
,∠APM=30°,在Rt△ACM中,AM=2,∠MAC=∠APM=30°,
CM=AM•sin30°=2×
 =1,AC=AM•cos30°=2×
=1,AC=AM•cos30°=2×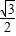 =
=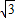 ,
,∴OC=OM-CM=3-1=2,A(2,
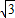 ),
),∵A、B两点关于x轴对称,
∴B(2,-
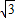 ),
),∵抛物线过P(-1,0)、M(3,0),设抛物线解析式为y=a(x+1)(x-3),
将B(2,-
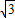 )代入,得a(2+1)(2-3)=-
)代入,得a(2+1)(2-3)=-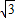 ,解得a=
,解得a=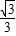 ,
,∴y=
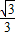 (x+1)(x-3)=
(x+1)(x-3)=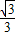 x2-
x2-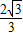 x-
x-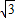 ;
;(2)如图1,过Q点作QH⊥x轴,垂足为H,由(1)得H(x,0),Q(x,
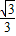 x2-
x2-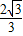 x-
x-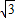 )
)S四边形APQB=S△APC+S△PQH+S梯形BCHQ=
 ×PC×AC+
×PC×AC+ ×PH×QH+
×PH×QH+ ×(QH+BC)×CH
×(QH+BC)×CH=
 ×3×
×3×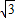 +
+ ×(x+1)×(-
×(x+1)×(-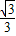 x2+
x2+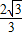 x+
x+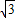 )+
)+ ×(
×(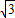 -
-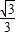 x2+
x2+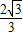 x+
x+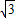 )×(2-x)
)×(2-x)=-
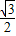 x2+
x2+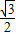 x+4
x+4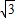 ,
,∵-
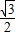 <0,四边形APQB的面积有最大值,
<0,四边形APQB的面积有最大值,当x=
 时,四边形APQB的面积最大值为
时,四边形APQB的面积最大值为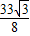 ,此时Q(
,此时Q( ,-
,-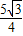 );
);(3)直线AF与弧AE′B相切.如图2,连接AE,
由(1)可知,
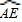 度数为60°,根据对称性可知
度数为60°,根据对称性可知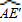 度数为60°,△AEE′为等边三角形,
度数为60°,△AEE′为等边三角形,∴
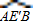 的圆心为E点,∠EAF=∠EAC+∠CAF=30°+60°=90°,
的圆心为E点,∠EAF=∠EAC+∠CAF=30°+60°=90°,∴直线AF与弧AE′B相切.
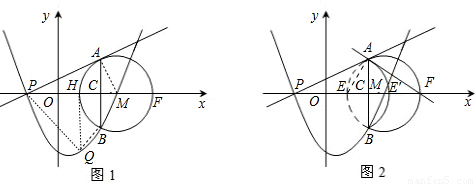
点评:本题考查了二次函数解析式的确定、图形面积的求法、圆心角定理、切线的性质与判定、特殊三角形的判定和性质等知识点.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′; 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为

 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为. ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),