题目内容
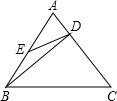如图，在正三角形ABC中，D，E分别在AC，AB上，且| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
分析：根据两边对应成比例且夹角相等的两个三角形相似，可判定△AED∽△CBD．
解答：解：∵AD：AC=1：3，
∴AD：DC=1：2；
∵△ABC是正三角形，
∴AB=BC=AC；
∵AE=BE，
∴AE：BC=AE：AB=1：2
∴AD：DC=AE：BC；
∵∠A为公共角，
∴△AED∽△CBD；
故选B．
∴AD：DC=1：2；
∵△ABC是正三角形，
∴AB=BC=AC；
∵AE=BE，
∴AE：BC=AE：AB=1：2
∴AD：DC=AE：BC；
∵∠A为公共角，
∴△AED∽△CBD；
故选B．
点评：考查相似三角形的判定定理：
（1）两角对应相等的两个三角形相似；
（2）两边对应成比例且夹角相等的两个三角形相似；
（3）三边对应成比例的两个三角形相似．
（1）两角对应相等的两个三角形相似；
（2）两边对应成比例且夹角相等的两个三角形相似；
（3）三边对应成比例的两个三角形相似．
练习册系列答案
中考解读考点精练系列答案
相关题目
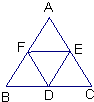
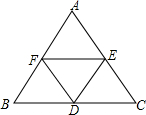如图，在正三角形ABC中，D、E、F分别为BC、CA、AB的中点，请你数一数，有
12、如图，在正三角形ABC中，点D，E分别AB，AC在上，且DE∥BC，如果BC=12cm，AD：DB=1：3，那么三角形ADE的周长=
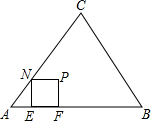已知△ABC是正三角形，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上．