题目内容
10、如图，在正三角形ABC中，D、E、F分别为三边BC、CA、AB的中点，则图中共有菱形（ ）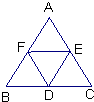
分析：由题意知，DF，EF，DE是等边三角形的中位线，根据三角形的中位线平行于对边且等于对边的一半知，有DF=EF=ED=AE=AF=BF=CE=BD=CD，根据四边相等的四边形是菱形判定作答．
解答：解：∵D、E、F分别为三边BC、CA、AB的中点，
∴DF=EF=ED=AE=AF=BF=CE=BD=CD，
∴有3个菱形：菱形AEDF，菱形BDEF，菱形CDFE．
故选B．
∴DF=EF=ED=AE=AF=BF=CE=BD=CD，
∴有3个菱形：菱形AEDF，菱形BDEF，菱形CDFE．
故选B．
点评：本题考查了等边三角形的性质和三角形中位线的性质及菱形的判定．菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
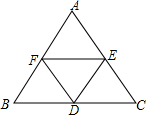如图，在正三角形ABC中，D、E、F分别为BC、CA、AB的中点，请你数一数，有
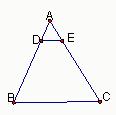12、如图，在正三角形ABC中，点D，E分别AB，AC在上，且DE∥BC，如果BC=12cm，AD：DB=1：3，那么三角形ADE的周长=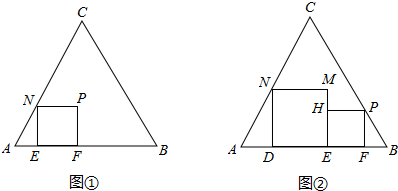
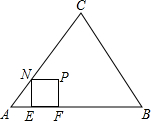已知△ABC是正三角形，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上．