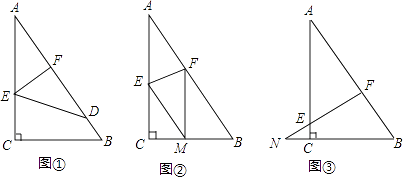题目内容
【题目】如图，在ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG=CH．
【答案】证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADF=∠CFH，∠EAG=∠FCH，
∵E、F分别为AD、BC边的中点，
∴AE=DE= 
AD，CF=BF= BC，
∴DE∥BF，DE=BF，
∴四边形BFDE是平行四边形，
∴BE∥DF，
∴∠AEG=∠ADF，
∴∠AEG=∠CFH，
在△AEG和△CFH中，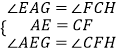 
，
∴△AEG≌△CFH（ASA），
∴AG=CH．
【解析】本题考查了平行四边形的性质和判定，全等三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形全等是解决问题的关键．根据平行四边形的性质得到AD∥BC，得出∠ADF=∠CFH，∠EAG=∠FCH，证出四边形BFDE是平行四边形，得出BE∥DF，证出∠AEG=∠CFH，由ASA证明△AEG≌△CFH，得出对应边相等即可．
练习册系列答案
相关题目
【题目】东坡商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为p= 
且其日销售量y（kg）与时间t（天）的关系如表：
时间t（天） | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y（kg） | 118 | 114 | 108 | 100 | 80 | 40 | … |
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的前24天中，公司决定每销售1kg水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
