题目内容
 24、已知,梯形ABCD中,AD∥BC,M为BC上一点,若将△ABM绕点M顺时针旋转一定角度,恰好与△CDM重合.
24、已知,梯形ABCD中,AD∥BC,M为BC上一点,若将△ABM绕点M顺时针旋转一定角度,恰好与△CDM重合.(1)在上述旋转过程中,旋转角为图中的哪个角?
请在横线上直接填出答案:
∠BMD
;(2)小明发现△MAD为等腰三角形,请你帮他说明理由;
(3)本题中,你还有什么发现?请写出一条,并说明理由.
分析:(1)△ABM绕点M顺时针旋转一定角度,恰好与△CDM重合,易得∠BMD;
(2)因为AD∥BC,可求得∠MAD=∠MDA,MA=MD,即可求证△MAD为等腰三角形;
(3)根据旋转的性质,可发现M为BC的中点.
(2)因为AD∥BC,可求得∠MAD=∠MDA,MA=MD,即可求证△MAD为等腰三角形;
(3)根据旋转的性质,可发现M为BC的中点.
解答:解:(1)∠BMD;
(2)∵AD∥BC,
∴∠BMA=∠MAD,∠DMC=∠MDA,
由旋转知∠BMA=∠DMC,
∴∠MAD=∠MDA,
∴MA=MD,即△MAD为等腰三角形;
(3)M为BC的中点;
∵△ABM绕点M顺时针旋转一定角度,恰好与△CDM重合,
∴BM=CM,
∴M为BC的中点.
(2)∵AD∥BC,
∴∠BMA=∠MAD,∠DMC=∠MDA,
由旋转知∠BMA=∠DMC,
∴∠MAD=∠MDA,
∴MA=MD,即△MAD为等腰三角形;
(3)M为BC的中点;
∵△ABM绕点M顺时针旋转一定角度,恰好与△CDM重合,
∴BM=CM,
∴M为BC的中点.
点评:本题考查旋转的性质--旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
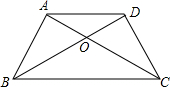 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.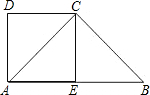 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( ) 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )