Question

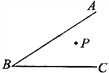
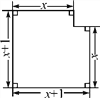
【题目】如图，在平面直角坐标系中，边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第四象限，直线BD与反比例函数的图象交于点B、E.

（1）求反比例函数及直线BD的解析式；

（2）求点E的坐标；

（3）连结、、，求△的面积.

Answer 1

【答案】（1）反比例函数解析式： ，直线BD的解析式： ；（2）E（-2,1）；（3）4.

【解析】试题分析:（1）根据正方形的边长，正方形关于y轴对称，可得点A、B、D的坐标，根据待定系数法，可得函数解析式；
（2）根据两个函数解析式，可的方程组，根据解方程组，可得答案．

（3）如图，连接EC，求出EC的解析式为y=-3x-5，再求出直线与x轴的交点P的坐标（，0），分别求出ΔEPA和ΔCPA的面积即可得解.

试题解析：（1）边长为2的正方形ABCD关于y轴对称，边在AD在x轴上，点B在第四象限，C在第三象限，
∴A（1，0），D（-1，0），B（1，-2），C（1-，-2）．
∵反比例函数y=的图象过点B，
∴=-2，k=-2，
∴反比例函数解析式为y=-，
设直线BD的解析式为y=kx+b，
∴，解得．
直线BD的解析式y=-x-1；
（2）∵直线BD与反比例函数y=的图象交于点E，
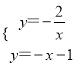∴，解得或，
∵B（1，-2），
∴E（-2，1）．

（3）连接EC交x轴于点P，设EC所在的直线解析式为：y=kx+b，则有：

解得：

故EC所在直线解析式为：y=-3x-5.

当y=0时，x=-

∴AP=

∴SΔEAC=SΔEPA+SΔCPA=.