题目内容
【题目】(1)已知![]() ,求
,求![]() 的最小值.
的最小值.
爱思考的小思想到了一种方法:先用![]() 表示
表示![]() 得:
得:![]() _____;
_____;
再把![]() 代入
代入![]() 得到:
得到:![]() ______;
______;
再利用配方法得到:![]() (
(![]() _____)
_____)![]() +______;
+______;
根据完全平方式的非负性,就得到了![]() 的最小值是______.
的最小值是______.
请你补充完成小思的解答过程:
(2)根据小思的方法,请你求出:当![]() 时,求出
时,求出![]() 的最小值.
的最小值.
(3)但是假如变成![]() ,求
,求![]() 的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
则 ,
,
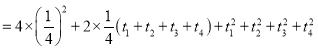 ,
,
![]() .
.
故![]() 的最小值是
的最小值是![]() .
.
参考小喻的方法,当![]() 时,
时,
求出![]() 的最小值.
的最小值.
【答案】(1)1-b, (1-b)+b,![]() ,
,![]() ,
, ![]() ;(2)50;(3)
;(2)50;(3) ![]() .
.
【解析】
(1)根据完全平方式的非负性解答即可;
(2)把x+y=10变形后,代入x+y求解即可;
(3) 先设![]() ,再根据
,再根据![]() ,把
,把![]() 变形解答即可.
变形解答即可.
解:(1) ∵ ![]() ,∴a=1-b, ∴a+b=(1-b)+b∴a+b=2b-2b+1=2(b-
,∴a=1-b, ∴a+b=(1-b)+b∴a+b=2b-2b+1=2(b-![]() )+
)+![]() ,
,
∴![]() 的最小值是
的最小值是![]() ;
;
(2) ∵![]() ,∴x=10-y, ∴x+y=(10-y)+y=2y-20y+100=2(y-5)+50, ∴x+y的最小值为:50;.
,∴x=10-y, ∴x+y=(10-y)+y=2y-20y+100=2(y-5)+50, ∴x+y的最小值为:50;.
(3) 设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() =
=![]()
=2019·![]() +2·
+2·![]()
![]() +
+![]()
=![]() +
+![]() ≥
≥![]() ,
,
∴![]() 的最小值是
的最小值是![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
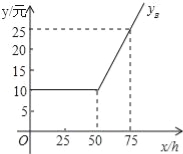
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
【题目】如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,

(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律,计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.








