题目内容
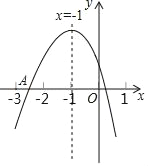
【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，下列结论中：
①abc＜0；②9a﹣3b+c＜0；③b2﹣4ac＞0；④a＞b，
正确的结论是_____（只填序号）
【答案】②③④
【解析】
运用二次函数的图形与性质进行判断即可.
解析:①因为抛物线开口向下,所以a<0.因为抛物线的对称轴为直线x=-1＜0, b＜0,因为抛物线与y轴的交点在y轴正半轴上,所以c>0.所以abc>0.故①错误;
②因为由图像得当x=一3时,y＜0,所以9a-3b+c<0.故②正确;
③因为图像与z轴有两个交点,所以b2﹣4ac＞0.故③正确;
④因为抛物线的对称轴为直线x=-1,
,b=2a
所以a-b=a-2a=-a＞0,所以a>b.故④正确.
故正确的有②③④，
故答案：②③④.
练习册系列答案
相关题目
【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.
