Question

【题目】综合题：探索发现规律拓展应用题
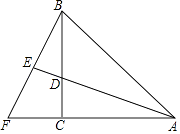
（1）如图①，∠CEF=90°，点B在射线EF上，AB∥CD，若∠ABE=130°，求∠C的度数；

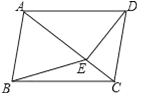
（2）如图②，把“∠CEF=90°”改为“∠CEF=120°”，点B在射线EF上，AB∥CD．猜想∠ABE与∠C的数量关系，并说明理由．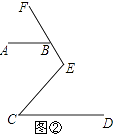

Answer 1

【答案】
（1）解：如图①，

过E作EK∥AB，则∠ABE+∠1=180°，

∴∠1=180°﹣∠ABE=50°，

∵∠CEF=90°，

∴∠2=90°﹣∠1=40°，

∵AB∥CD，EK∥AB，

∴EK∥CD，

∴∠C=∠2=40°

（2）解：∠ABE﹣∠C=60°，

理由：如图②，

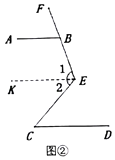
过E作EK∥AB，则∠ABE+∠1=180°，

∴∠1=180°﹣∠ABE，

∵AB∥CD，EK∥AB，

∴EK∥CD，

∴∠C=∠2，

∵∠CEF=∠1+∠2=120°，即180°﹣∠ABE+∠C=120°，

∴∠ABE﹣∠C=180°﹣120°=60°

【解析】（1）由小题1发现隐藏的规律：平行线间出现折线时，过折点作平行线，构造同旁内角和内错角;（2）类比运用此规律可以解决小题2.
【考点精析】根据题目的已知条件，利用平行线的性质的相关知识可以得到问题的答案，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．