��Ŀ����
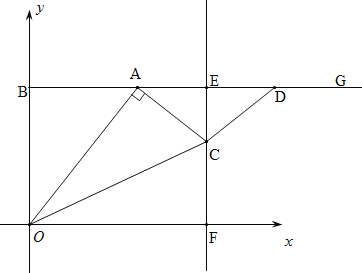
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�B��0��8��Ϊ�˵������BG��x�ᣬ��A������BG�ϵ�һ�����㣨��A���B���غϣ���������AG��ȡAD=OB�����߶�AD�Ĵ�ֱƽ���ߣ�����ΪE������x�ύ�ڵ�F������A��AC��OA��������EF�ڵ�C������OC��CD�����A�ĺ�����Ϊt��
��1���ú�t��ʽ�ӱ�ʾ��E������Ϊ_______��
��2����tΪ��ֵʱ����OCD=180����
��3������C���F���غ�ʱ������OCF�����ΪS����S��t֮��ĺ�������ʽ��
���𰸡���1��E��![]() ��8������2��
��8������2��![]() ����3��
����3��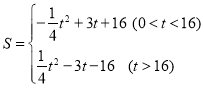 ��
��
��������
�����������1����AD=OB=8���õ�AE=ED=4�����ɵ�A�ĺ�����Ϊt���õ���E�����ꣻ
��2������OCD=180��ʱ����ͼ1����EC��BO���õ�![]() ����EC=
����EC=![]() ��������AEC�ס�OBA���õ�
��������AEC�ס�OBA���õ�![]() ���Ӷ�EC=
���Ӷ�EC=![]() ����
����![]() =
=![]() ���ⷽ�̼������t��ֵ��
���ⷽ�̼������t��ֵ��
��3����C��F�غ�ʱ���ɣ�2���ã�![]() =8�����t=16���ʷ�����������ۣ���
=8�����t=16���ʷ�����������ۣ���![]() ����
����![]() ������
������![]() ��OF=BE=
��OF=BE=![]() ��ֻ��Ҫ��ʾ��CF���빫ʽ���ɣ�
��ֻ��Ҫ��ʾ��CF���빫ʽ���ɣ�
�����������1����AD=OB=8����AE=ED=4������A�ĺ�����Ϊt����E��![]() ��8����
��8����
��2������OCD=180��ʱ����ͼ1����EC��BO����![]() ����
����![]() ����EC=
����EC=![]() ����AC��OA�����1+��2=90�����ߡ�2+��3=90�������1=��3���ߡ�AEC=��ABO�����AEC�ס�OBA����
����AC��OA�����1+��2=90�����ߡ�2+��3=90�������1=��3���ߡ�AEC=��ABO�����AEC�ס�OBA����![]() ����
����![]() ����EC=
����EC=![]() ����
����![]() =
=![]() ����
����![]() ����ã�
����ã�![]() ��
��![]() ����ȥ������t=
����ȥ������t=![]() ��
��

��3����C��F�غ�ʱ���ɣ�2���ã�![]() =8�����t=16����������������ۣ���
=8�����t=16����������������ۣ���![]() ����
����![]() ��
��
����![]() ʱ����ͼ2���ɣ�2���ã�EC=
ʱ����ͼ2���ɣ�2���ã�EC=![]() ����CF=
����CF=![]() ����OF=BE=
����OF=BE=![]() ����
����![]() ����
����![]() ��
��
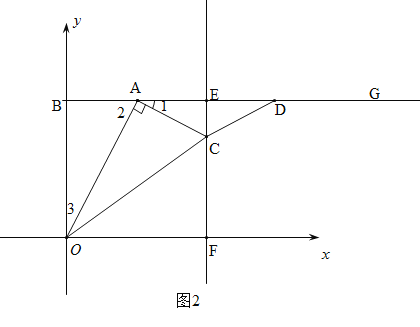
����![]() ʱ����ͼ3���ɣ�2���ã�EC=
ʱ����ͼ3���ɣ�2���ã�EC=![]() ����CF=
����CF=![]() ����OF=BE=
����OF=BE=![]() ��
��
��![]() ����
����![]() ��
��

����������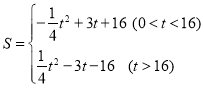 ��
��

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�