题目内容
【题目】如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
【答案】
(1)
证明:如图所示:连接OF、OC,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,
∴AO=![]() AD,EC=
AD,EC=![]() BC,
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,
∴AE∥OC,
∴∠DOC=∠OAF,∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
∵在△ODC和△OFC中
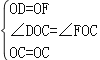 ,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(2)
解:如图所示:连接DE,
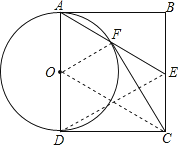
∵AO=DO,AF=EF,AD=2,
∴DE=20F=2,
∵E是BC的中点,
∴EC=1,
在Rt△DCE中,由勾股定理得:
DC=![]() ,
,
∴AB=CD=![]() .
.
【解析】(1)利用平行四边形的判定方法得出四边形OAEC是平行四边形,进而得出△ODC≌△OFC(SAS),求出OF⊥CF,进而得出答案;
(2)利用勾股定理得出DC的长,即可得出AB的长,
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
相关题目