Question

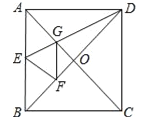
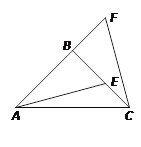
【题目】如图，△ABC中，AB=BC,∠ABC=90°,F为AB延长线上一点，点E在BC上，且AE=CF.

（1）求证:△ABE≌△CBF；

（2）若,AE=2,求△ACF的周长.

Answer 1

【答案】（）见解析；（2）++3.

【解析】试题分析：

试题解析：

（1）证明：∵∠ABC=90°,

∴∠FBC=90°.

在Rt△ABE和Rt△CBF中,

∵AB=BC, AE=CF,

∴Rt△ABE≌Rt△CBF(HL).

（2）∵∠ABC=90°,AB=BC,∴∠BAC=45°,

∵∠CAE=15°,

∴∠BAE=30°,

又∵AE=2,

∴BE=1,AB=

∴AC=.

∵△ABE≌△CBF,

∴BF=BE=1,FC=AE=2,

∴AF=+1.

∴C△ACF=AF+AC+FC=+1++2=++3.