题目内容
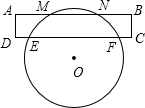 如图所示,矩形ABCD与⊙O相交于M、N、F、E,若AM=2,DE=1,EF=8,则MN的长为
如图所示,矩形ABCD与⊙O相交于M、N、F、E,若AM=2,DE=1,EF=8,则MN的长为
- A.2
- B.4
- C.6
- D.8
C
分析:过O作OH⊥CD并延长,交AB于P,求出DH的长,再根据矩形的性质求出MP的长,再由垂径定理解答即可.
解答: 解:过O作OH⊥CD并延长,交AB于P,则EH=
解:过O作OH⊥CD并延长,交AB于P,则EH= EF=
EF= ×8=4,
×8=4,
DH=DE+EH=1+4=5,即AP=5,MP=AP-AM=5-2=3,MN=2MP=2×3=6.
故选C.
点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形求解.
分析:过O作OH⊥CD并延长,交AB于P,求出DH的长,再根据矩形的性质求出MP的长,再由垂径定理解答即可.
解答:
 解:过O作OH⊥CD并延长,交AB于P,则EH=
解:过O作OH⊥CD并延长,交AB于P,则EH= EF=
EF= ×8=4,
×8=4,DH=DE+EH=1+4=5,即AP=5,MP=AP-AM=5-2=3,MN=2MP=2×3=6.
故选C.
点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形求解.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
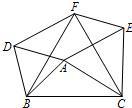 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
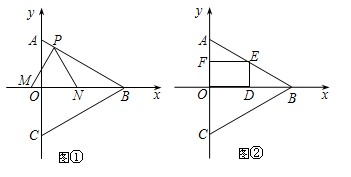
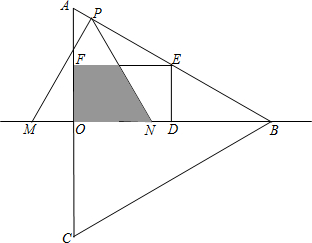 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.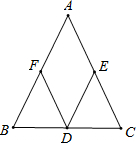 (2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )
(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )