题目内容
已知抛物线y=ax2-4ax+4a-2,其中a是常数.(1)求抛物线的顶点坐标;
(2)若a>
| 2 | 5 |
分析:(1)已知抛物线的解析式为y=ax2-4ax+4a-2,把其化为顶点式,从而求出抛物线的顶点坐标;
(2)由题意a>
,根据公式法求出ax2-4ax+4a-2=0的根,再由题意抛物线与x轴交于整数点(坐标为整数的点),来确定a的值,从而求出抛物线的解析式.
(2)由题意a>
| 2 |
| 5 |
解答:解:(1)依题意,得a≠0,
∴y=ax2-4ax+4a-2=a(x2-4x+4)-2=a(x-2)2-2;
∴抛物线的顶点坐标为(2,-2);(2分)
(2)∵抛物线与x轴交于整数点,
∴ax2-4ax+4a-2=0的根是整数,
∴x=
=2±
是整数,
∵a>0,x=2±
是整数;(3分)
∴
是整数的完全平方数.∵a>
,
∴
<5,(4分)
∴
取1,4,
当
=1时,a=2;当
=4时,a=
.
∴a的值为2或
,
∴抛物线的解析式为y=2x2-8x+6或y=
x2-2x.(6分)
∴y=ax2-4ax+4a-2=a(x2-4x+4)-2=a(x-2)2-2;
∴抛物线的顶点坐标为(2,-2);(2分)
(2)∵抛物线与x轴交于整数点,
∴ax2-4ax+4a-2=0的根是整数,
∴x=
4a±
| ||
| 2a |
| ||
| a |
∵a>0,x=2±
|
∴
| 2 |
| a |
| 2 |
| 5 |
∴
| 2 |
| a |
∴
| 2 |
| a |
当
| 2 |
| a |
| 2 |
| a |
| 1 |
| 2 |
∴a的值为2或
| 1 |
| 2 |
∴抛物线的解析式为y=2x2-8x+6或y=
| 1 |
| 2 |
点评:此题主要考查一元二次方程与函数的关系及用公式法求出方程的根.

练习册系列答案
相关题目
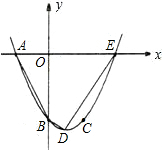 与x轴的另一个交点为E.
与x轴的另一个交点为E.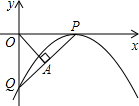 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=