题目内容
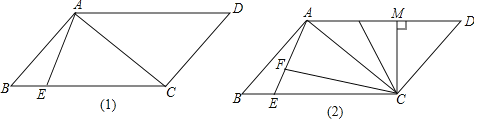
【题目】如图,在![]() 中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
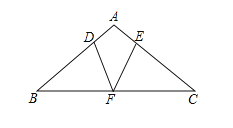
(1)求证:△BDF≌△CEF.
(2)当∠A= 100°,BD=BF时,求∠DFE的度数。
【答案】(1)见解析 (2)40°
【解析】
(1)由∠ADF=∠AEF可得∠BDF=∠FEC,根据中点的定义可知:BF=CF,结合已知条件,由AAS可以判定△BDF≌OCEF.
(2)由(1)可得AABC是等腰三角形,又由BD=BF可求出∠BDF=∠BFD=70°,从而求出∠DFE的度数.
证明:(1)∵∠ADF=∠AEF,
∴∠BDF=∠FEC,
∵F为BC的中点,
∴BF=CF,
又∵∠B=∠C
∴△BDF≌△CEF(AAS)
(2)∵∠A=100°,
∴∠B=∠C=40°,
∵BD=BF,
∴∠BDF=∠BFD=70°,
∵△BDF≌△CEF,
∴∠EFC=70°,
∴∠DFE=40°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?