题目内容
 如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是
如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是
- A.①②④
- B.②③
- C.①③④
- D.①②③④
C
分析:①连接CF,CD.运用弦切角定理过渡到证明内错角相等,从而证明平行;
②FC=CE= BC;
BC;
③根据射影定理证明DE•AG=AB•EC;
④根据∠BCD=90°,则BD是直径,又弧AB=弧BC,根据垂径定理的推论有弧AD=弧CD.
解答: 解:①连接CF,CD,
解:①连接CF,CD,
∵⊙O2与BC相切于C,
∴CD是直径,
∴∠CFD=90°,
∵F是AC的中点,
∴∠GCF=∠FCA=60°,
∴∠DCE=∠DCF=30°,
∴∠EDC=∠FDC=60°,
∴CE=CF,∠CEF=∠CFE,
∵⊙O2与BC相切于C
∴∠FCG=∠FEC
∴∠FCG=∠EFC
∴EF∥BC,故正确;
②∵EF∥BC
∴∠CEF=60°
∴三角形CEF是等边三角形
∴FC=CE= BC,故错误;
BC,故错误;
③根据EF∥BC,CD⊥EF,得CD⊥CG,
∴CD是小圆的直径,则∠CFD=90°,
根据直角三角形CDG中的射影定理,得CF2=DF•DG,
再结合上述的证明结论,即可得到DE•AG=AB•EC,故正确;
④根据∠BCD=90°,得BD是大圆的直径,
∵等边三角形△ABC内接于⊙O1,
∴∠ABD=∠CBD,
∴弧AD=弧DC,故正确.
故选C.
点评:综合运用了切线的性质、圆周角定理的推论、三角形的中位线定理等.注意:上一个结论可以被下面所用.
分析:①连接CF,CD.运用弦切角定理过渡到证明内错角相等,从而证明平行;
②FC=CE=
 BC;
BC;③根据射影定理证明DE•AG=AB•EC;
④根据∠BCD=90°,则BD是直径,又弧AB=弧BC,根据垂径定理的推论有弧AD=弧CD.
解答:
 解:①连接CF,CD,
解:①连接CF,CD,∵⊙O2与BC相切于C,
∴CD是直径,
∴∠CFD=90°,
∵F是AC的中点,
∴∠GCF=∠FCA=60°,
∴∠DCE=∠DCF=30°,
∴∠EDC=∠FDC=60°,
∴CE=CF,∠CEF=∠CFE,
∵⊙O2与BC相切于C
∴∠FCG=∠FEC
∴∠FCG=∠EFC
∴EF∥BC,故正确;
②∵EF∥BC
∴∠CEF=60°
∴三角形CEF是等边三角形
∴FC=CE=
 BC,故错误;
BC,故错误;③根据EF∥BC,CD⊥EF,得CD⊥CG,
∴CD是小圆的直径,则∠CFD=90°,
根据直角三角形CDG中的射影定理,得CF2=DF•DG,
再结合上述的证明结论,即可得到DE•AG=AB•EC,故正确;
④根据∠BCD=90°,得BD是大圆的直径,
∵等边三角形△ABC内接于⊙O1,
∴∠ABD=∠CBD,
∴弧AD=弧DC,故正确.
故选C.
点评:综合运用了切线的性质、圆周角定理的推论、三角形的中位线定理等.注意:上一个结论可以被下面所用.

练习册系列答案
相关题目
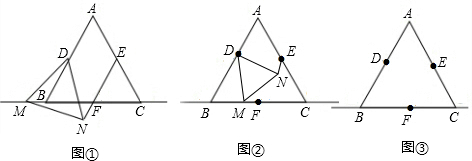
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.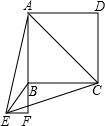 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想. 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动