题目内容
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
(1)随着二氧化碳排放量的减少,每排放一吨二氧化碳,企业相应获得的利润也有所提高,且相应获得的利润p(万元)与月份x(月)的函数关系如图所示,那么哪月份,该企业获得的月利润最大?最大月利润是多少万元?
(2)受国家政策的鼓励,该企业决定从6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,与此同时,每排放一吨二氧化碳,企业相应获得的利润在上一个月的基础上都增加50%,要使今年6、7月份月利润的总和是今年5月份月利润的3倍,求a的值(精确到个位).
(参考数据: =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,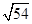 =7.35)
=7.35)
(1)5,4000;(2)13.
解析试题分析:(1)根据图象可以知道利润p(万元)与月份x是一次函数关系,并且随着月份的增加利润也增加,首先根据图象确定利润p与x的函数关系,然后利用函数的增减性即可确定今年哪月份,该企业获得的月利润最大?最大月利润是多少万元;
(2)由于该企业决定从今年6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,与此同时,每排放一吨二氧化碳,企业相应获得的利润在上一个月的基础上都增加50%.
试题解析:(1)根据图象知道当x=1,p=80,
当x=4,p=95,
设p=kx+b,
∴  ,解得
,解得 ,
,
∴p=5x+75;根据k>0,y随x增大而增大,
∴当x=5时,p最大,p=5×5+75=100万元;
∴5月份的利润是:100万×40=4000万元;
(2)(2)∵该企业决定从今年6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,
而当x=5时,y=40,
∴6月份的二氧化碳排放量为40(1-a%),
7月份的二氧化碳排放量为40(1-a%)2,
5月份的利润为4000万元,
∴6月份的利润为100(1+50%)×40(1-a%),
7月份的利润为100(1+50%)×(1+50%)×40(1-a%)2,
∴100(1+50%)×40(1-a%)+100(1+50%)×(1+50%)×40(1-a%)2=3×4000,
∴a=13.
考点:二次函数的应用.

 的方程:
的方程: ①和
①和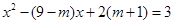 ②,其中
②,其中 .
. 的图象与
的图象与 、
、 两点(点
两点(点 处,点
处,点 处,若点
处,若点 的值;
的值; ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 的值是________________.
的值是________________.

 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线 经过A,C两点,与
经过A,C两点,与 轴的另一交点为D.
轴的另一交点为D.
 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标; ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点; 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.

 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
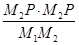 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.