题目内容
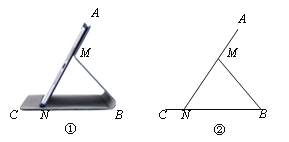
【题目】用如图1中的长方形和正方形纸板作侧面和底面，做成如图2的紧式和横式的两种无盖纸盒.现存仓库里有m张长方形纸板和n张正方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则m+n的值可能是( )
A.2017B.2018C.2019D.2020
【答案】D
【解析】
此题的等量关系为：横式无盖纸盒需要的正方形的总个数+竖式无盖纸盒的正方形的总个数=n；横式无盖纸盒需要的长方形的总个数+竖式无盖纸盒的长方形的总个数=m，设竖式长方体纸盒有x个，横式纸盒y个，列方程组，求出x+y的值，根据x+y的值是正整数且是5的倍数，可得出答案.
解：设竖式长方体纸盒有x个，横式纸盒y个，根据题意得：
由①+②得：5x+5y=n+m
∴x+y=
∵x、y为正整数，
∴为正整数，且m+n是5的倍数
∴m+n可能的值为2020
故答案为：D
练习册系列答案
相关题目
