题目内容
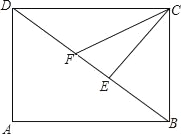
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
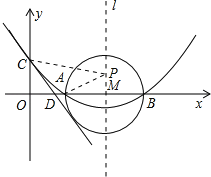
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
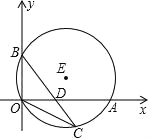
(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
【答案】解:(1)由题意,设抛物线的解析式为![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)∴![]() ,解得:
,解得:![]() 。
。
∴抛物线的解析式为![]() ,即:
,即:![]() 。
。
令y=0时,![]() ,解得:x=2或x=6。
,解得:x=2或x=6。
∴A(2,0),B(6,0)。
(2)存在。
如图1,由(1)知:抛物线的对称轴l为x=4,
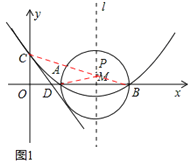
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小。
∵B(6,0),C(0,2),∴OB=6,OC=2。∴BC=2![]() 。
。
∴AP+CP=BC=2![]() 。
。
∴AP+CP的最小值为2![]() 。
。
(3)如图2,连接ME,
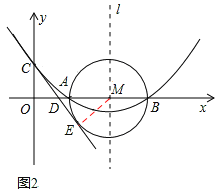
∵CE是⊙M的切线,∴ME⊥CE,∠CEM=90°。
由题意,得OC=ME=2,∠ODC=∠MDE,
∵在△COD与△MED中,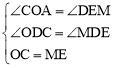 ,
,
∴△COD≌△MED(AAS)。∴OD=DE,DC=DM。
设OD=x,则CD=DM=OM﹣OD=4﹣x,
∵在Rt△COD中,OD2+OC2=CD2,∴![]() ,解得x=
,解得x=![]() 。
。
∴D(![]() ,0)。
,0)。
设直线CE的解析式为y=kx+b,
∵直线CE过C(0,2),D(![]() ,0)两点,
,0)两点,
则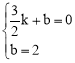 ,解得:
,解得: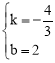 。
。
∴直线CE的解析式为![]() 。
。
【解析】
试题(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标。
(2)根据轴对称的性质,线段BC的长即为AP+CP的最小值。
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在Rt△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可。

 寒假乐园北京教育出版社系列答案
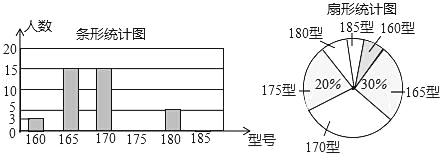
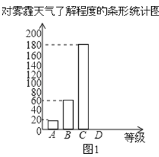
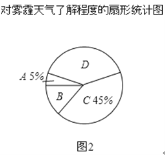
寒假乐园北京教育出版社系列答案【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.