Question

【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1，0)，点B(x2，0)，(点A在点B的左侧)，抛物线的对称轴为直线x=-1．

(1)若点A的坐标为(-3，0)，求抛物线的表达式及点B的坐标；

(2)C是第三象限的点，且点C的横坐标为-2，若抛物线恰好经过点C，直接写出x2的取值范围；

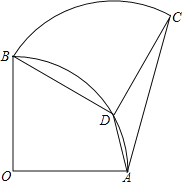
(3)抛物线的对称轴与x轴交于点D，点P在抛物线上，且∠DOP=45°，若抛物线上满足条件的点P恰有4个，结合图象，求a的取值范围．

Answer 1

【答案】（1），（1，0）；（2）-1＜x2＜0；（3）a＜-2．

【解析】

（1）由题意可知抛物线的对称轴为，求出b=2a，将点A的坐标代入抛物线的表达式，即可求解；

（2）根据题意可得点C在第三象限，即点A在点C和函数对称轴之间，故-2＜x1＜-1，继而进行分析即可求解；

（3）根据题意可得满足条件的P在x轴的上方有2个，在x轴的下方也有2个，则抛物线与y轴的交点在x轴的下方，即可求解．

解：（1）抛物线的对称轴为，解得：b=2a，

故y=ax2+bx+a+2=a（x+1）2+2，

将点A的坐标代入上式并解得：，

故抛物线的表达式为：；

令y=0，即，解得：x=-3或1，

故点B的坐标为：（1，0）.

（2）由（1）知：，

点C在第三象限，即点C在点A的下方，

即点A在点C和函数对称轴之间，故-2＜x1＜-1，

而，即x2=-2-x1，

故-1＜x2＜0.

（3）∵抛物线的顶点为（-1，2），

∴点D（-1，0），

∵∠DOP=45°，若抛物线上满足条件的点P恰有4个，

∴抛物线与x轴的交点在原点的左侧，如下图，

∴满足条件的P在x轴的上方有2个，在x轴的下方也有2个，

则抛物线与y轴的交点在x轴的下方，

当x=0时，，

解得：a＜-2，

故a的取值范围为：a＜-2．