题目内容
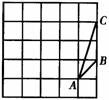
 如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1,B1,C1三点都在格点上),并求出这个三角形的面积.
如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1,B1,C1三点都在格点上),并求出这个三角形的面积.分析:如图可得出AC=
,则AC的对应边A1C1最长的长度为
,所以可依次作出A1B1,B1C1.即△A1B1C1,△A1B1C1的面积可用相似比求解.
| 10 |
| 50 |
解答: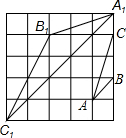 解:利用勾股定理得出△ABC各边长AB=
解:利用勾股定理得出△ABC各边长AB=
,BC=2,AC=
,
故AC的对应边A1C1最长的长度为
×
=
=5
,
则A1C1=5
,A1B1=
,B1C1=2
.
∵
=
=
,
∴
=
=5,
∵S△ABC=
×1×2=1,
∴△A1B1C1的面积为:5.
 解:利用勾股定理得出△ABC各边长AB=
解:利用勾股定理得出△ABC各边长AB=| 2 |
| 10 |
故AC的对应边A1C1最长的长度为
| 5 |
| 10 |
| 50 |
| 2 |
则A1C1=5
| 2 |
| 10 |
| 5 |
∵
| A1C1 |
| AC |
| ||
|
| 5 |
∴
| S△A1B1C1 |
| S△ABC |
| (A1C1)2 |
| (AC)2 |
∵S△ABC=
| 1 |
| 2 |
∴△A1B1C1的面积为:5.
点评:本题考查了位似图形的意义及作图能力.解题的关键是根据AC=
,找到AC的对应边最长的长度为
.
| 10 |
| 50 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 77、阅读材料后再解答问题
77、阅读材料后再解答问题