题目内容
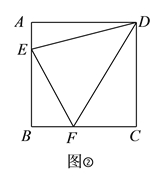
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.


(![]() )求该抛物线的函数解析式.
)求该抛物线的函数解析式.
(![]() )点
)点![]() 在抛物线上,连接
在抛物线上,连接![]() 、
、![]() .试问,在对称轴左侧的抛物线上是否存在一点
.试问,在对称轴左侧的抛物线上是否存在一点![]() ,满足
,满足![]() ?如果存在,请求出点
?如果存在,请求出点![]() 点的坐标;如果不存在,请说明理由.
点的坐标;如果不存在,请说明理由.
【答案】(![]() )
)![]() (
(![]() )
)![]()
【解析】(1)把![]() ,
, ![]() 代入
代入![]() ,运用待定系数法求二次函数的解析式;(2)先求出D、C的坐标,然后证明△CDB≌△CQB,得出Q的坐标求得BQ的解析式,再设点
,运用待定系数法求二次函数的解析式;(2)先求出D、C的坐标,然后证明△CDB≌△CQB,得出Q的坐标求得BQ的解析式,再设点![]() 在
在![]() 上,得出关于m的一元二次方程解出m即可得解.
上,得出关于m的一元二次方程解出m即可得解.
解:(![]() )
)![]() ,
, ![]() 代入
代入![]() ,
,
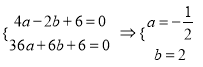 ,
,
∴![]() .
.
(![]() )
)![]() 代入抛物线上,得
代入抛物线上,得![]() ,
, ![]() ,
,
存在点![]() ,使得
,使得![]() ,
,
设![]() 与
与![]() 轴交
轴交![]() ,
,
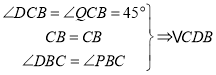 ≌
≌![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
![]() ,
, 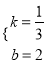
∴![]() ,
,
设![]() 在
在![]() 上,
上,
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴![]() ,
, ![]() (舍),
(舍),
∴![]() .
.
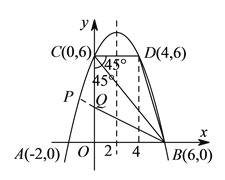
“点睛”本题主要考查的是二次函数的综合应用,解答关键是应用待定系数法求二次函数的解析式,全等三角形的性质和判定,二次函数轴对称的性质进行解题.

练习册系列答案
相关题目
【题目】为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表
级别 | 指数 | 天数 | 百分比 |
优 | 0﹣50 | 24 | m |
良 | 51﹣100 | a | 40% |
轻度污染 | 101﹣150 | 18 | 15% |
中度污染 | 151﹣200 | 15 | 12.5% |
重度污染 | 201﹣300 | 9 | 7.5% |
严重污染 | 大于300 | 6 | 5% |
合计 | 120 | 100% |
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a= ,m= ;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是 度;
(4)请通过计算估计郑州市2017年中空气质量指数大于100的天数.