题目内容
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
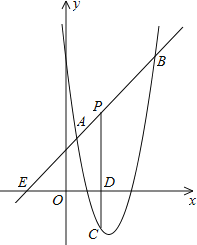
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
【答案】(1)抛物线的解析式y=2x2﹣8x+6;(2)存在.当n=![]() 时,线段PC有最大值
时,线段PC有最大值![]() .
.
【解析】
试题分析:(1)将点B坐标代入直线解析式,求出m的值,然后把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;
(2)设动点P的坐标为(n,n+2),点C的坐标为(n,2n2﹣8n+6),表示出PC的长度,然后利用配方法求出二次函数的最大值,并求出此时n的值.
解:(1)∵B(4,m)在直线y=x+2上,
∴m=6,即B(4,6),
∵A(![]() ,
,![]() )和B(4,6)在抛物线y=ax2+bx+6上,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴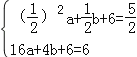 ,
,
解得:![]() ,
,
∴抛物线的解析式y=2x2﹣8x+6;
(2)存在.
设动点P的坐标为(n,n+2),点C的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4=﹣2(n﹣![]() )2+
)2+![]() ,
,
∵﹣2<0,
∴开口向下,有最大值,
∴当n=![]() 时,线段PC有最大值
时,线段PC有最大值![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目