题目内容
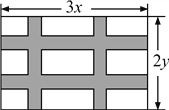
【题目】如图,要设计一幅长为3xcm、宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是多少?
【答案】6xy-6ax-4by+4ab(cm2)
【解析】试题分析:此题可将彩条平移到如图所示的长方形的靠边处,则空白部分组成一个长方形,这个大长方形长(3x-2b)cm,宽为(2y-2a),则空白部分的面积=长×宽即可得出.
试题解析:

可设想将彩条平移到如图所示的长方形的靠边处,将9个小矩形组合成“整体”,
一个大的空白长方形,则该长方形的面积就是空白区域的面积.
而这个大长方形长(3x2b)cm,宽为(2y2a)cm.
所以空白区域的面积为(3x2b)(2y2a)cm2.
即(6xy-6ax-4by+4ab)cm2.

练习册系列答案
相关题目
【题目】父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 |
|
|
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
【题目】某超市为方便顾客购买,将瓜子放入包装袋内出售,其质量x(kg)与售价y(元)之间的关系如下表(售价中的0.10元是包装袋的费用):
质量x/kg | 售价y/元 |
1 | 15.00+0.10 |
2 | 30.00+0.10 |
3 | 45.00+0.10 |
4 | 60.00+0.10 |
…… | …… |
(1)观察表格,写出y与x之间的关系式.
(2)买8 kg这种瓜子需花费多少元?
(3)用100元去买这种瓜子,最多能买多少千克?

