Question

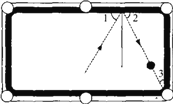
【题目】如图回答以下问题

(1) 若，可以得到哪两条线段平行？直接填空： ∥ （不用说明理由）

(2) 在(1)的结论下，如果，又能得到哪两条线段平行，请说明理由．

(3) 在（2）的结论下,如果于，30°，求的度数.

Answer 1

【答案】（1）DE∥BC，（2）DC∥FG， （3）60°

【解析】试题分析：（1）∠DEC+∠ACB=180°可以证明DE∥BC，（同旁内角互补，两直线平行）；

（2）由DE∥BC可得∠1=∠DCB（两直线平行，内错角相等），又∠1=∠2，那么∠2=∠DCB，所以DC∥FG（同位角相等，两线平行）．

（3）由CD∥FG，得到∠FGB=∠CDB=90°，根据直角三角形两锐角互余即可得到结论．

试题解析：解：（1）DE∥BC；

（2）可得DC∥FG．理由如下：

∵由（1）得DE∥BC，∴∠1=∠DCB ．

又∵∠1=∠2，∴∠2=∠DCB，∴DC∥FG．

（3）∵CD⊥AB于D，∴∠CDB=90°．

∵CD∥FG，∴∠FGB=∠CDB=90°．∵30°，∴∠2=90°-60°．