题目内容
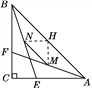
【题目】如图,在△ABC中,∠C=90°,CA=CB,E,F分别为CA,CB上一点,CE=CF,M,N分别为AF,BE的中点,求证:AE=![]() MN.
MN.

【答案】证明见解析.
【解析】试题分析:取AB的中点H,连接MH、NH,根据三角形的中位线平行于第三边并且等于第三边的一半可得NH=![]() AE,NH∥AE,MH=
AE,NH∥AE,MH=![]() BF,MH∥BF,再求出AE=BF,∠MHN=90°,判断出△MNG是等腰直角三角形,根据等腰直角三角形的性质可得NH=
BF,MH∥BF,再求出AE=BF,∠MHN=90°,判断出△MNG是等腰直角三角形,根据等腰直角三角形的性质可得NH=![]() MN,再表示出AE即可得证.
MN,再表示出AE即可得证.
试题解析:如图,取AB的中点H,连接MH,NH,则MH=![]() BF,
BF,
NH=![]() AE.
AE.
∵CE=CF,CA=CB,∴AE=BF.∴MH=NH.
∵点M,N,N分别为AF,AB,BE的中点,
∴MH∥BF,NH∥AE.
∴∠AHM=∠ABC,∠BHN=∠BAC.
∴∠MHN=180°-(∠AHM+∠BHN)=180°-(∠ABC+∠BAC)=90°.∴NH=![]() MN.
MN.
∴AE=2NH=2×![]() MN=
MN=![]() MN.
MN.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目