题目内容
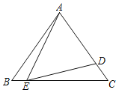
【题目】如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的位置关系.
【答案】AD⊥EF，且AD平分EF，理由见解析.
【解析】
根据角平分线的性质得到∠EAD=∠FAD，DE=DF，易证△AED≌△AFD，从而得到AE=AF，然后可证△AEG≌△AFG，得到EG=FG，∠AGE=∠AGF=90°，从而得出结论.
解：AD⊥EF，且AD平分EF，理由如下：
∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F
∴∠EAD=∠FAD，DE=DF，∠AED=∠AFD=90°，
在△AED和△AFD中，
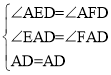
∴△AED≌△AFD（AAS）
∴AE=AF
在△AEG和△AFG中，
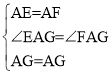
∴△AEG≌△AFG（SAS）
∴EG=FG，∠AGE=∠AGF=90°
即AD⊥EF，且AD平分EF.
练习册系列答案
出彩同步大试卷系列答案
相关题目
