题目内容
【题目】如图,在△ABC中,∠ACB=90°.小聪同学利用直尺和圆规完成了如下作图:
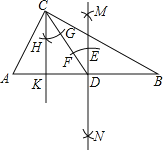
①分别以点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
②连接CD,以点D为圆心,以一定长为半径画弧,交MN于点E,交CD于点F,以点C为圆心,以同样定长为半径画弧,与CD交于点G,以点G为圆心,以EF长为半径画弧与前弧交于点H.作射线CH与AB交于点K,请根据以上操作,解答下列问题
(1)由尺规作图可知:直线MN是线段AB的 线,∠DCK= .
(2)若CD=5,AK=2,求CK的长.
【答案】(1)垂直平分,∠CDM;(2)CK=4.
【解析】
(1)利用基本作图(作线段的垂直平分线和作一个角等于已知角)填空;
(2)先利用CD为斜边上的中线得到AD=CD=BD=5.则DK=3,再利用∠DCK=∠CDM得到CK∥MN,所以∠CKD=∠MDB=90°,然后利用勾股定理计算CK的长.
(1)由作法得直线MN是线段AB的垂直平分线,∠DCK=∠CDM;
故答案为垂直平分;∠CDM;
(2)∵∠ACB=90°,AD=BD,
∴AD=CD=BD=5.
∴DK=AD﹣AK=3,
∵∠DCK=∠CDM,
∴CK∥MN,
∴∠CKD=∠MDB=90°,
∴CK=![]() =
=![]() =4.
=4.

练习册系列答案
相关题目