��Ŀ����
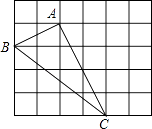
����Ŀ����ͼ��ʾ������һ�ű߳�Ϊ4��������ֽƬABCD����PΪ������AD���ϵ�һ�㣨�����A����D�غϣ���������ֽƬ�۵���ʹ��B����P������C����G����PG��DC��H���ۺ�ΪEF������BP��BH�� 
��1����֤����APB=��BPH��
��2������P�ڱ�AD���ƶ�ʱ����PDH���ܳ��Ƿ����仯����֤����Ľ��ۣ�
��3����APΪx���ı���EFGP�����ΪS�����S��x�ĺ�����ϵʽ������S�Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��֤������ͼ1����PE=BE��
���EBP=��EPB��
�֡ߡ�EPH=��EBC=90�㣬
���EPH����EPB=��EBC����EBP��
����PBC=��BPH��
�֡�AD��BC��
���APB=��PBC��
���APB=��BPH
��2����PHD���ܳ�����Ϊ��ֵ8��
֤������ͼ2����B��BQ��PH������ΪQ��

�ɣ�1��֪��APB=��BPH��
�ڡ�ABP�͡�QBP�� 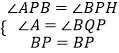 ��
��
���ABP�ա�QBP��AAS����
��AP=QP��AB=BQ��
�֡�AB=BC��
��BC=BQ��
�֡ߡ�C=��BQH=90�㣬BH=BH��
���BCH�ա�BQH��
��CH=QH��
���PHD���ܳ�Ϊ��PD+DH+PH=AP+PD+DH+HC=AD+CD=8
��3����ͼ3����F��FM��AB������ΪM��
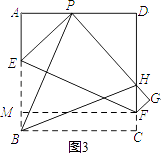
��FM=BC=AB��
�֡�EFΪ�ۺۣ�
��EF��BP��
���EFM+��MEF=��ABP+��BEF=90�㣬
���EFM=��ABP��
�֡ߡ�A=��EMF=90�㣬
���EFM�ա�PBA��ASA����
��EM=AP=x��
����Rt��APE����4��BE��2+x2=BE2��
��ã� ![]() ��
��
�� ![]() ��
��
�֡��۵������ʵó��ı���EFGP���ı���BEFCȫ�ȣ�
�� ![]() ��
��
���� ![]() ��
��
�䷽�ã� ![]() ��
��
�൱x=2ʱ��S����Сֵ6��
����������1�����ݷ��۱任�����ʵó���PBC=��BPH����������ƽ���ߵ����ʵó���APB=��PBC���ɵó��𰸣���2������֤����ABP�ա�QBP�������ó���BCH�ա�BQH�����ɵó�PD+DH+PH=AP+PD+DH+HC=AD+CD=8����3��������֪�ó���EFM�ա�BPA������������Rt��APE�У���4��BE��2+x2=BE2 �� ���ö��κ�������ֵ������ɣ�
�����㾫����������Ҫ�����˶��κ�������ֵ�������ε����ʵ����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a���������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������β�����ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�