题目内容
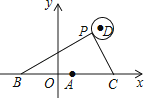
【题目】如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2= ![]() (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号).
(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号). 
【答案】①③④
【解析】解:∵抛物线y1=a(x+2)2+m与抛物线y2= ![]() (x﹣3)2+n的对称轴分别为x=﹣2,x=3, ∴两条抛物线的对称轴距离为5,故①正确;
(x﹣3)2+n的对称轴分别为x=﹣2,x=3, ∴两条抛物线的对称轴距离为5,故①正确;
∵y1=a(x+2)2+m经过点A(1,3)与原点,
∴ ![]() ,
,
解得 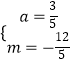 ,
,
∴y1= ![]() (x+2)2﹣
(x+2)2﹣ ![]() ,
,
∵y2= ![]() (x﹣3)2+n经过点A(1,3),
(x﹣3)2+n经过点A(1,3),
∴ ![]() (1﹣3)2+n=3,
(1﹣3)2+n=3,
解得n=1,
∴y2= ![]() (x﹣3)2+1,
(x﹣3)2+1,
当x=0时,y= ![]() (0﹣3)2+1=5.5,故②错误;
(0﹣3)2+1=5.5,故②错误;
由图象得,当x>1时,y1>y2 , 故③正确;
∵过点A作x轴的平行线,分别交两条抛物线于点B,C,
∴令y=3,则 ![]() (x+2)2﹣
(x+2)2﹣ ![]() =3,
=3,
整理得,(x+2)2=9,
解得x1=﹣5,x2=1,
∴AB=1﹣(﹣5)=6,
∴A(1,3),B(﹣5,3);
令y=3,则 ![]() (x﹣3)2+1=3,
(x﹣3)2+1=3,
整理得,(x﹣3)2=4,
解得x1=5,x2=1,
∴C(5,3),
∴AC=5﹣1=4,
∴BC=10,
∴y轴是线段BC的中垂线,故④正确.
所以答案是①③④.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目