Question

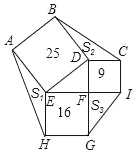
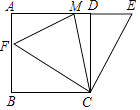
【题目】如图，四边形ABCD为正方形，边长为4，E为AD延长线上一点，DE=x（0＜x＜4），在AE上取一点M，连接CM，将△CME沿CM对折，若点E恰落在线段AB上的点F处，则AM= ．

Answer 1

【答案】
【解析】解：∵四边形ABCD是正方形，

∴AB=BC=CD=AD=4，

∵△CMF是由△CME翻折得到，

∴CF=CE，ME=MF，

在Rt△BCF和Rt△DCE中，

，

∴Rt△BCF≌Rt△DCE，

∴BF=DE=x，设AM=y，

在Rt△AFM中，∵AF=4﹣x，MF=ME=4﹣y+x，AM=x，

∴（4﹣x）2+y2=（4﹣y+x）2，

解得y= ．

所以答案是

【考点精析】本题主要考查了正方形的性质和翻折变换（折叠问题）的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．