题目内容
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .分别以点
.分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若点
.若点![]() 是
是![]() 的中点,
的中点,![]() 的周长为8,则
的周长为8,则![]() 的长为( )
的长为( )

A.2B.3C.4D.5
【答案】A
【解析】
根据平行线的性质可得∠FAC=∠BCA,∠DAB+∠ABC=180°,可得∠DAB=∠ADC,利用ASA可证明△AOF≌△COB,可得AF=BC=3,即可证明四边形ABCD是等腰梯形,可得AB=CD,根据作图可知点E在线段AC的垂直平分线上,由点O为AC中点可得BE是AC的垂直平分线,可得AF=FC,AB=BC,即可求出FC=CD=BC=3,根据△CDF的周长求出DF的长即可.
∵AD//BC,
∴∠FAC=∠ACB,∠DAB+∠ABC=180°,
∵![]() ,
,
∴∠DAB=∠ADC,
∴四边形ABCD是等腰梯形,
∴AB=CD,
∵点O为AC中点,
∴OA=OC,
在△AOF和△COB中,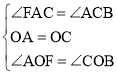 ,
,
∴△AOF≌△COB,
∴AF=BC=3,
∵以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,
,
∴点E在线段AC的垂直平分线上,
∵点O是AC中点,![]() 交
交![]() 于点
于点![]() ,
,
∴BE是AC的垂直平分线,
∴AF=FC,AB=BC,
∴FC=CD=BC=3,
∵△CDF的周长是8,
∴DF=8-CF-CD=2,
故选A.

练习册系列答案
相关题目