МвДүДЪИЭ
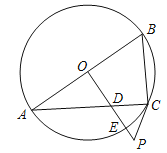
ҰңМвДүҰүИзНәӘ¬ФЪRtҰчABCЦРӘ¬ҰПACBӘҢ90ҰгӘ¬ACӘҢ16Ә¬BCӘҢ12Ә¬µгDҰұE·Ц±рОҒ±ЯABҰұBCЦРµгӘ¬µгPөУµгAіц·ұӘ¬СШЙдПЯAB·ҢПтТФГүГл5ёцµӨО»і¤¶ИµДЛЩ¶ИПтµгBФЛ¶ҮӘ¬µҢµгBНӘЦ№Ә®µ±µгPІ»УлµгAЦШғПК±Ә¬№эµгPЧчPQҰОACӘ¬ЗТµгQФЪЦ±ПЯABЧуІаӘ¬APӘҢPQӘ¬№эµгQЧчQMҰНABҢ»ЙдПЯABУЪµгMӘ®ЙиµгPФЛ¶ҮµДК±әдОҒtӘЁГлӘ©
ӘЁ1Ә©УГғ¬tµДөъКэКҢ±нКңПЯ¶ОDMµДі¤¶ИӘ»
ӘЁ2Ә©Зуµ±µгQВдФЪBC±ЯЙПК±tµДЦµӘ»
ӘЁ3Ә©ЙиҰчPQMУлҰчDEBЦШµюІү·ЦНәРОµДГж»эОҒSӘЁЖҢ·ҢµӨО»Ә©Ә¬µ±ҰчPQMУлҰчDEBУРЦШµюЗТЦШµюІү·ЦНәРОКЗИэҢЗРОК±Ә¬ЗуSУлtµДғҮКэ№ШПµКҢӘ»
ӘЁ4Ә©µ±ң№эµгCғНҰчPQMЦРТ»ёц¶ӨµгµДЦ±ПЯЖҢ·ЦҰчPQMµДДЪҢЗК±Ә¬Ц±ҢУРөіцөЛК±tµДЦµӘ®

Ұңөр°ёҰүӘЁ1Ә©µ±0ӘәtҰЬ![]() К±Ә¬DMӘҢ©Ѓ9t+10Ә¬µ±
К±Ә¬DMӘҢ©Ѓ9t+10Ә¬µ±![]() ӘәtҰЬ4К±Ә¬DMӘҢ9t©Ѓ10Ә»ӘЁ2Ә©
ӘәtҰЬ4К±Ә¬DMӘҢ9t©Ѓ10Ә»ӘЁ2Ә©![]() sӘ»ӘЁ3Ә©µ±
sӘ»ӘЁ3Ә©µ±![]() ӘәtҰЬ
ӘәtҰЬ![]() К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ¬SӘ©ӘҢ
К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ¬SӘ©ӘҢ![]() t2©Ѓ
t2©Ѓ![]() t+
t+![]() Ә®µ±
Ә®µ±![]() ҰЬtҰЬ4К±Ә¬ SӘҢ6t2©Ѓ48t+96Ә®ӘЁ4Ә©tµДЦµОҒ
ҰЬtҰЬ4К±Ә¬ SӘҢ6t2©Ѓ48t+96Ә®ӘЁ4Ә©tµДЦµОҒ![]() s»т
s»т![]() sӘ®
sӘ®
ҰңҢвОцҰү
ӘЁ1Ә©·ЦµгMФЪПЯ¶ОADЙП»тµгMФЪПЯ¶ОADµДСУі¤ПЯК±БҢЦЦЗйРО·Ц±рЗуҢвӘ®
ӘЁ2Ә©µ±µгQВдФЪBCЙПК±Ә¬УЙPQҰОACӘ¬үЙµГ![]() Ә¬УЙөЛ№№ҢЁ·ҢіМәөүЙҢвңцОКМвӘ®
Ә¬УЙөЛ№№ҢЁ·ҢіМәөүЙҢвңцОКМвӘ®
ӘЁ3Ә©·ЦБҢЦЦЗйРОӘғұЩИзНә3-1ЦРӘ¬µ±![]() ӘәtҰЬ
ӘәtҰЬ![]() К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ®ұЪИзНә3-2ЦРӘ¬µ±
К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ®ұЪИзНә3-2ЦРӘ¬µ±![]() ҰЬtҰЬ4К±Ә¬ЦШµюІү·ЦКЗҰчPBKӘ¬·Ц±рЗуҢвӘ®ӘЁ4Ә©·ЦБҢЦЦЗйРОӘғұЩИзНә4-1ЦРӘ¬µ±Ц±ПЯCQЖҢ·ЦҰПPQMК±Ә¬ЙиЦ±ПЯCQҢ»ABУЪGӘ¬ЧчGKҰНPQУЪKӘ®АыУГИ«µИИэҢЗРОµДРФЦКӘ¬ЖҢРРПЯ·ЦПЯ¶ОіЙ±ИАэ¶ЁАнӘ¬№№ҢЁ·ҢіМәөүЙӘ®ұЪИзНә4-2ЦРӘ¬µ±CMЖҢ·ЦҰПQMPК±Ә¬ЧчCGҰНABУЪGӘ®ЗуіцAMµДі¤Ә¬№№ҢЁ·ҢіМәөүЙҢвңцОКМвӘ®
ҰЬtҰЬ4К±Ә¬ЦШµюІү·ЦКЗҰчPBKӘ¬·Ц±рЗуҢвӘ®ӘЁ4Ә©·ЦБҢЦЦЗйРОӘғұЩИзНә4-1ЦРӘ¬µ±Ц±ПЯCQЖҢ·ЦҰПPQMК±Ә¬ЙиЦ±ПЯCQҢ»ABУЪGӘ¬ЧчGKҰНPQУЪKӘ®АыУГИ«µИИэҢЗРОµДРФЦКӘ¬ЖҢРРПЯ·ЦПЯ¶ОіЙ±ИАэ¶ЁАнӘ¬№№ҢЁ·ҢіМәөүЙӘ®ұЪИзНә4-2ЦРӘ¬µ±CMЖҢ·ЦҰПQMPК±Ә¬ЧчCGҰНABУЪGӘ®ЗуіцAMµДі¤Ә¬№№ҢЁ·ҢіМәөүЙҢвңцОКМвӘ®
ҢвӘғӘЁ1Ә©ИзНә1ЦРӘ¬

ФЪRtABCЦРӘ¬ҰЯACӘҢ16Ә¬BCӘҢ12Ә¬ҰПCӘҢ90ҰгӘ¬
ҰаABӘҢ![]() Ә¬
Ә¬
ҰЯPQҰОACӘ¬
ҰаҰПAӘҢҰПQPMӘ¬
ҰЯҰПCӘҢҰПPMQӘҢ90ҰгӘ¬
ҰаҰчACBҰЧҰчPMQӘ¬
Ұа![]() ,
,
Ұа![]() ,
,
ҰаPMӘҢ4tӘ¬MQӘҢ3tӘ¬
µ±0ӘәtҰЬ![]() К±Ә¬DMӘҢAD©ЃAMӘҢ10©Ѓ5t©Ѓ4tӘҢ©Ѓ9t+10Ә®
К±Ә¬DMӘҢAD©ЃAMӘҢ10©Ѓ5t©Ѓ4tӘҢ©Ѓ9t+10Ә®
µ±![]() ӘәtҰЬ4К±Ә¬DMӘҢAM©ЃADӘҢ9t©Ѓ10Ә®
ӘәtҰЬ4К±Ә¬DMӘҢAM©ЃADӘҢ9t©Ѓ10Ә®
ӘЁ2Ә©ИзНә2ЦРӘ¬

µ±µгQВдФЪBCЙПК±Ә¬ҰЯPQҰОACӘ¬
Ұа![]() ,
,
Ұа![]() Ә¬
Ә¬
ҢвµГtӘҢ![]() Ә¬
Ә¬
Ұаµ±µгQВдФЪBC±ЯЙПК±tµДЦµОҒ![]() sӘ®
sӘ®
ӘЁ3Ә©ИзНә3©Ѓ1ЦРӘ¬µ±![]() ӘәtҰЬ
ӘәtҰЬ![]() К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ¬SӘҢ
К±Ә¬ЦШµюІү·ЦКЗҰчDMKӘ¬SӘҢ![]() ҰБDMҰБMKӘҢ
ҰБDMҰБMKӘҢ![]() ҰБӘЁ9t©Ѓ10Ә©ҰБ
ҰБӘЁ9t©Ѓ10Ә©ҰБ![]() ӘЁ9t©Ѓ10Ә©ӘҢ
ӘЁ9t©Ѓ10Ә©ӘҢ![]() t2©Ѓ
t2©Ѓ![]() t+
t+![]() Ә®
Ә®

ИзНә3©Ѓ2ЦРӘ¬µ±![]() ҰЬtҰЬ4К±Ә¬ЦШµюІү·ЦКЗҰчPBKӘ¬SӘҢ
ҰЬtҰЬ4К±Ә¬ЦШµюІү·ЦКЗҰчPBKӘ¬SӘҢ![]() PKBKӘҢ
PKBKӘҢ![]() ҰБ
ҰБ![]() ӘЁ20©Ѓ5span>tӘ©
ӘЁ20©Ѓ5span>tӘ©![]() ӘЁ20©Ѓ5tӘ©ӘҢ6t2©Ѓ48t+96Ә®
ӘЁ20©Ѓ5tӘ©ӘҢ6t2©Ѓ48t+96Ә®

ӘЁ4Ә©ИзНә4©Ѓ1ЦРӘ¬µ±Ц±ПЯCQЖҢ·ЦҰПPQMК±Ә¬ЙиЦ±ПЯCQҢ»ABУЪGӘ¬ЧчGKҰНPQУЪKӘ®
ҰЯҰПQKGӘҢҰПQMGӘҢ90ҰгӘ¬ҰПGQKӘҢҰПGQMӘ¬QGӘҢQGӘ¬
ҰаҰчQGKҰХҰчQGMӘЁAASӘ©Ә¬
ҰаQKӘҢQMӘҢ3tӘ¬PKӘҢPQ©ЃQKӘҢ5t©Ѓ3tӘҢ2tӘ¬
ҰаPGӘҢ![]() PKӘҢ
PKӘҢ![]() tӘ¬
tӘ¬
ҰЯPQҰОACӘ¬
Ұа![]() Ә¬
Ә¬
Ұа Ә¬
Ә¬
ҰаtӘҢ![]() Ә®
Ә®
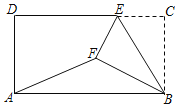
ИзНә4©Ѓ2ЦРӘ¬µ±CMЖҢ·ЦҰПQMPК±Ә¬ЧчCGҰНABУЪGӘ®

ҰЯ![]() ACBCӘҢ
ACBCӘҢ![]() ABCGӘ¬
ABCGӘ¬
ҰаCGӘҢ![]() Ә¬AGӘҢ
Ә¬AGӘҢ Ә¬
Ә¬
ҰЯҰПCMGӘҢҰПGCMӘҢ45ҰгӘ¬
ҰаCGӘҢGMӘҢ![]() Ә¬
Ә¬
ҰаAMӘҢ9tӘҢ![]() Ә¬
Ә¬
ҢвµГtӘҢ![]() Ә¬
Ә¬
ЧЫЙПЛщКцӘ¬ВъЧгМхәюµДtµДЦµОҒ![]() s»т
s»т![]() sӘ®
sӘ®

 ФД¶БүміµПµБРөр°ё
ФД¶БүміµПµБРөр°ёҰңМвДүҰүБәғГµДТыКі¶ФС§ЙъµДЙнМеҰұЦЗБ¦·ұУэғНҢҰүµЖрµҢБЛә«ЖдЦШТҒµДЧчУГӘ¬»зІЛЦРµ°°ЧЦКҰұёЖҰұБЧә°Ц¬ИЬРФО¬ЙъЛШУЕУЪЛШКіӘ¬¶шЛШКіЦРІ»±ӨғНЦ¬·ңЛбҰұО¬ЙъЛШғНПЛО¬ЛШУЦУЕУЪ»зКіӘ¬Ц»УР»зКіУлЛШКіККµ±өоЕдӘ¬ІЕДЬЗү»ҮіхЦРЙъµДЙнМеЛШЦКӘ®ДіРӘОҒБЛБЛҢвС§ЙъµДМеЦКҢҰүµЧөүцӘ¬ТФ±гКіМГОҒС§ЙъМṩғПАнЙЕКіӘ¬¶Ф±ңРӘЖЯДкә¶Ұұ°ЛДкә¶С§ЙъµДМеЦКҢҰүµЧөүцҢшРРБЛµчІйӘ¬№эіМИзПВӘғ
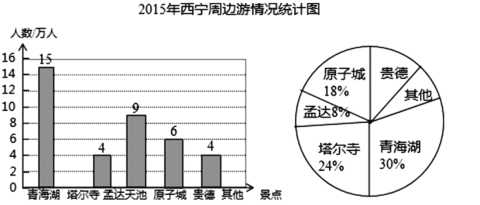
КХәҮКэңЭӘғөУЖЯҰұ°ЛДкә¶БҢёцДкә¶ЦРёчійИҰ15ГыС§ЙъӘ¬ҢшРРБЛМеЦКҢҰүµІвКФӘ¬ІвКФіЙәЁӘЁ°Щ·ЦЦЖӘ©ИзПВӘғ
ЖЯДкә¶Әғ74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
°ЛДкә¶Әғ81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
ХыАнКэңЭӘғ
Дкә¶ | xӘә60 | 60ҰЬxӘә80 | 80ҰЬxӘә90 | 90ҰЬxҰЬ100 |
ЖЯДкә¶ | 0 | 10 | 4 | 1 |
°ЛДкә¶ | 1 | 5 | 8 | 1 |
ӘЁЛµГчӘғ90·Цә°ТФЙПОҒУЕРгӘ¬80Ұ«90·ЦӘЁІ»ғ¬90·ЦӘ©ОҒБәғГӘ¬60Ұ«80·ЦӘЁІ»ғ¬80·ЦӘ©ОҒә°ёсӘ¬60·ЦТФПВОҒІ»ә°ёсӘ©
·ЦОцКэңЭӘғ
Дкә¶ | ЖҢңщКэ | ЦРО»Кэ | ЦЪКэ |
ЖЯДкә¶ | ҰҰ ҰҰ | 75 | 75 |
°ЛДкә¶ | 77.5 | 80 | ҰҰ ҰҰ |
µГіцҢбВЫӘғ
ӘЁ2Ә©үЙТФНЖ¶ПіцҰҰ ҰҰДкә¶С§ЙъµДМеЦКҢҰүµЧөүцёьғГТ»Р©Ә¬ІұЛµГчАнУЙӘ»
ӘЁ3Ә©ИфЖЯДкә¶№ІУР300ГыС§ЙъӘ¬Зл№АәЖЖЯДкә¶МеЦКҢҰүµіЙәЁУЕРгµДС§ЙъИЛКэӘ®