题目内容
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
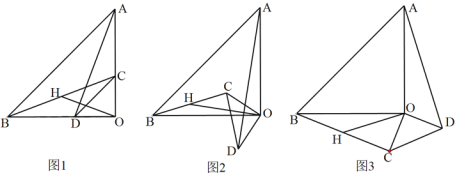
(1)如图1所示,求证:![]() 且
且![]()
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)首先证明△AOD≌△BOC(SAS),利用全等三角形的性质得到BC=AD,再利用直角三角形斜边中线的性质即可得到OH=![]() BC=
BC=![]() AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
(2)如图2中,延长OH到E,使得HE=OH,连接BE,通过证明△BEO≌△ODA,可得OH=![]() OE=
OE=![]() AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=
AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=![]() OE=
OE=![]() AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,

∴OC=OD,OA=OB,
在△AOD与△BOC中,
∵OA=OB,∠AOD=∠BOC,OD=OC,
∴△AOD≌△BOC(SAS),
∴BC=AD
∵H是BC中点,
∴OH=![]() BC=
BC=![]() AD.
AD.
∵△AOD≌△BOC
∴∠ADO=∠BCO,∠OAD=∠OBC,
∵点H为线段BC的中点,
∴∠OBH=∠HOB=∠OAD,
又∵∠OAD+∠ADO=90°,
∴∠ADO+∠BOH=90°,
∴OH⊥AD;
(2)解:结论:OH⊥AD,OH=![]() AD
AD

证明:如图2中,延长OH到E,使得HE=OH,连接BE,
易证△BEO≌△ODA,
∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOH=∠EOB+∠AOH=90°,
∴OH⊥AD.
如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA,

∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOG=∠EOB+∠AOG=90°,
∴∠AGO=90°,
∴OH⊥AD.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案