题目内容
(2013•安徽模拟)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
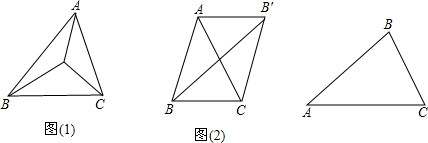
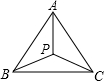
(1)如点P为锐角△ABC的费马点.且∠ABC=60°,PA=3,PC=4,求PB的长.
(2)如图(2),在锐角△ABC外侧作等边△ACB′连结BB′.求证:BB′过△ABC的费马点P,且BB′=PA+PB+PC.
(3)已知锐角△ABC,∠ACB=60°,分别以三边为边向形外作等边三角形ABD,BCE,ACF,请找出△ABC的费马点,并探究S△ABC与S△ABD的和,S△BCE与S△ACF的和是否相等.

(1)如点P为锐角△ABC的费马点.且∠ABC=60°,PA=3,PC=4,求PB的长.
(2)如图(2),在锐角△ABC外侧作等边△ACB′连结BB′.求证:BB′过△ABC的费马点P,且BB′=PA+PB+PC.
(3)已知锐角△ABC,∠ACB=60°,分别以三边为边向形外作等边三角形ABD,BCE,ACF,请找出△ABC的费马点,并探究S△ABC与S△ABD的和,S△BCE与S△ACF的和是否相等.
分析:(1)由题意可得△ABP∽△BCP,所以PB2=PA•PC,即PB=2
;
(2)在BB'上取点P,使∠BPC=120°,连接AP,再在PB'上截取PE=PC,连接CE.由此可以证明△PCE为正三角形,再利用正三角形的性质得到PC=CE,∠PCE=60°,∠CEB'=120°,而△ACB'为正三角形,由此也可以得到AC=B'C,∠ACB'=60°,现在根据已知的条件可以证明△ACP≌△B'CE,然后利用全等三角形的性质即可证明题目的结论;
(3)作CP平分∠ACB,交BC的垂直平分线于点P,P点即费马点;
要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
| 3 |
(2)在BB'上取点P,使∠BPC=120°,连接AP,再在PB'上截取PE=PC,连接CE.由此可以证明△PCE为正三角形,再利用正三角形的性质得到PC=CE,∠PCE=60°,∠CEB'=120°,而△ACB'为正三角形,由此也可以得到AC=B'C,∠ACB'=60°,现在根据已知的条件可以证明△ACP≌△B'CE,然后利用全等三角形的性质即可证明题目的结论;
(3)作CP平分∠ACB,交BC的垂直平分线于点P,P点即费马点;
要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
解答:解:(1)∵∠PAB+∠PBA=180°-∠APB=60°,
∠PBC+∠PBA=∠ABC=60°,
∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
∴
=
∴PB2=PA•PC=12,
∴PB=2
;
(2)证明:在BB'上取点P,使∠BPC=120°.连接AP,再在PB'上截取PE=PC,连接CE.
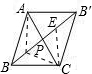
∠BPC=120°,
∴∠EPC=60°,
∴△PCE为正三角形,
∴PC=CE,∠PCE=60°,∠CEB'=120°.
∵△ACB'为正三角形,
∴AC=B′C,∠ACB'=60°,
∴∠PCA+∠ACE=∠ACE+∠ECB′=60°,
∴∠PCA=∠ECB′,
∴△ACP≌△B′CE,
∴∠APC=∠B′EC=120°,PA=EB′,
∴∠APB=∠APC=∠BPC=120°,
∴P为△ABC的费马点.
∴BB'过△ABC的费马点P,且BB'=EB'+PB+PE=PA+PB+PC.
(3)如下图,
作CP平分∠ACB,交BC的垂直平分线于点P,P点就是费马点;
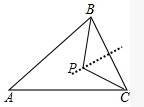
证明:过A作AM∥FC交BC于M,连接DM、EM,
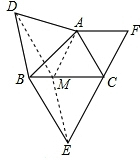
∵∠ACB=60°,∠CAF=60°,
∴∠ACB=∠CAF,
∴AF∥MC,
∴四边形AMCF是平行四边形,
又∵FA=FC,
∴四边形AMCF是菱形,
∴AC=CM=AM,且∠MAC=60°,
∵在△BAC与△EMC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△BAC≌△EMC,
∵∠DAM=∠DAB+∠BAM=60°+∠BAM
∠BAC=∠MAC+∠BAM=60°+∠BAM
∴∠BAC=∠DAM
在△ABC和△ADM中
AB=AD,∠BAC=∠DAM,AC=AM
∴△ABC≌△ADM(SAS)
故△ABC≌△MEC≌△ADM,
在CB上截取CM,使CM=CA,
再连接AM、DM、EM (辅助线这样做△AMC就是等边三角形了,后边证明更简便)
易证△AMC为等边三角形,
在△ABC与△MEC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△ABC≌△MEC(SAS),
∴AB=ME,∠ABC=∠MEC,
又∵DB=AB,
∴DB=ME,
∵∠DBC=∠DBA+∠ABC=60°+∠ABC,
∠BME=∠BCE+∠MEC=60°+∠MEC,
∴∠DBC=∠BME,
∴DB∥ME,
即得到DB与ME平行且相等,故四边形DBEM是平行四边形,
∴四边形DBEM是平行四边形,
∴S△BDM+S△DAM+S△MAC=S△BEM+S△EMC+S△ACF,
即S△ABC+S△ABD=S△BCE+S△ACF.
∠PBC+∠PBA=∠ABC=60°,
∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
∴
| PA |
| PB |
| PB |
| PC |
∴PB2=PA•PC=12,
∴PB=2
| 3 |

(2)证明:在BB'上取点P,使∠BPC=120°.连接AP,再在PB'上截取PE=PC,连接CE.

∠BPC=120°,
∴∠EPC=60°,
∴△PCE为正三角形,
∴PC=CE,∠PCE=60°,∠CEB'=120°.
∵△ACB'为正三角形,
∴AC=B′C,∠ACB'=60°,
∴∠PCA+∠ACE=∠ACE+∠ECB′=60°,
∴∠PCA=∠ECB′,
∴△ACP≌△B′CE,
∴∠APC=∠B′EC=120°,PA=EB′,
∴∠APB=∠APC=∠BPC=120°,
∴P为△ABC的费马点.
∴BB'过△ABC的费马点P,且BB'=EB'+PB+PE=PA+PB+PC.
(3)如下图,
作CP平分∠ACB,交BC的垂直平分线于点P,P点就是费马点;

证明:过A作AM∥FC交BC于M,连接DM、EM,

∵∠ACB=60°,∠CAF=60°,
∴∠ACB=∠CAF,
∴AF∥MC,
∴四边形AMCF是平行四边形,
又∵FA=FC,
∴四边形AMCF是菱形,
∴AC=CM=AM,且∠MAC=60°,
∵在△BAC与△EMC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△BAC≌△EMC,
∵∠DAM=∠DAB+∠BAM=60°+∠BAM
∠BAC=∠MAC+∠BAM=60°+∠BAM
∴∠BAC=∠DAM
在△ABC和△ADM中
AB=AD,∠BAC=∠DAM,AC=AM
∴△ABC≌△ADM(SAS)
故△ABC≌△MEC≌△ADM,
在CB上截取CM,使CM=CA,
再连接AM、DM、EM (辅助线这样做△AMC就是等边三角形了,后边证明更简便)
易证△AMC为等边三角形,
在△ABC与△MEC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△ABC≌△MEC(SAS),
∴AB=ME,∠ABC=∠MEC,
又∵DB=AB,
∴DB=ME,
∵∠DBC=∠DBA+∠ABC=60°+∠ABC,
∠BME=∠BCE+∠MEC=60°+∠MEC,
∴∠DBC=∠BME,
∴DB∥ME,
即得到DB与ME平行且相等,故四边形DBEM是平行四边形,
∴四边形DBEM是平行四边形,
∴S△BDM+S△DAM+S△MAC=S△BEM+S△EMC+S△ACF,
即S△ABC+S△ABD=S△BCE+S△ACF.
点评:此题考查了等腰三角形与等边三角形的性质及三角形内角和为180°等知识;此类已知三角形边之间的关系求角的度数的题,一般是利用等腰(等边)三角形的性质得出有关角的度数,进而求出所求角的度数.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
