题目内容
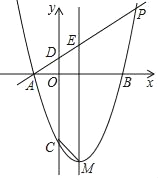
【题目】在平面直角坐标系xOy中,点P和图形W的“中点形”的定义如下:对于图形W上的任意一点Q,连结PQ,取PQ的中点,由所以这些中点所组成的图形,叫做点P和图形W的“中点形”.
已知C(-2,2),D(1,2),E(1,0),F(-2,0).
(1)若点O和线段CD的“中点形”为图形G,则在点![]() ,
,![]() ,
,![]() 中,在图形G上的点是 ;
中,在图形G上的点是 ;
(2)已知点A(2,0),请通过画图说明点A和四边形CDEF的“中点形”是否为四边形?若是,写出四边形各顶点的坐标,若不是,说明理由;
(3)点B为直线y=2x上一点,记点B和四边形CDEF的中点形为图形M,若图形M与四边形CDEF有公共点,直接写出点B的横坐标b的取值范围.
【答案】(1)![]() ,
,![]() ;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(
;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.
【解析】
(1)依照题意画出图形,观察图形可知点O和线段CD的中间点所组成的图形是线段C′D′,根据点A,C,D的坐标,利用中点坐标公式可求出点C′,D′的坐标,进而可得出结论;
(2)画出图形,观察图形可得出结论;
(3)利用一次函数图象上点的坐标特征可得出点B的坐标为(n,2n),依照题意画出图形,观察图形可知:点B和四边形CDEF的中间点只能在边EF和DE上,当点B和四边形CDEF的中间点在边EF上时,利用四边形CDEF的纵坐标的范围,可得出关于n的一元一次不等式组,解之即可得出n的取值范围;当点B和四边形CDEF的中间点在边DE上时,由四边形CDEF的横、纵坐标的范围,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.综上,此题得解.
解:(1)如图:点O和线段CD的中间点所组成的图形G是线段C′D′,
由题意可知:点C′为线段OC的中点,点D′为线段OD的中点.
∵点C的坐标为(-2,2),点D的坐标为(1,2),
∴点C′的坐标为(-1,1),点D′的坐标为(![]() ,1),
,1),
∴点O和线段CD的中间点所组成的图形G即线段C′D′的纵坐标是1,横坐标-1≤x≤![]() ,
,
∴点![]() ,
,![]() ,
,![]() 中,在图形G上的点是
中,在图形G上的点是![]() ,
,![]() ;
;
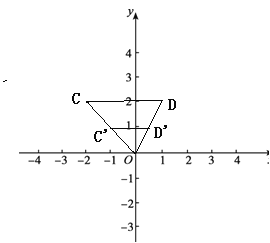
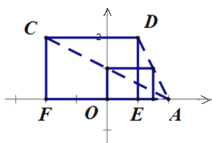
(2)点A和四边形CDEF的“中点形”是四边形.
各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1).
,1).
(3)∵点B的横坐标为b,
∴点B的坐标为(b,2b).
当点B和四边形CDEF的中间点在边EF上时,有![]() ,
,
解得:
当点B和四边形CDEF的中间点在边DE上时,有![]() ,
,
解得:1≤b≤2,
综上所述:点B的横坐标b的取值范围为-1≤b≤0 或 1≤b≤2.
故答案为:(1)![]() ,
,![]() ;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(
;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.

 53随堂测系列答案
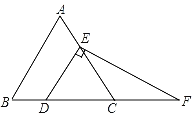
53随堂测系列答案【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
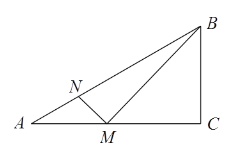
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
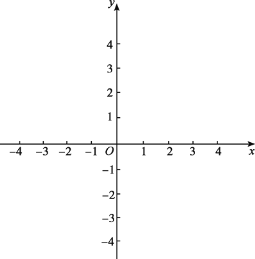
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).