题目内容
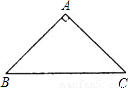
△ABC为等腰直角三角形，∠C=90°，D为BC上一点，且AD=2CD，则∠DAB=
- A.30°
- B.45°
- C.60°
- D.15°
D
分析：在Rt△ADC中，由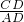
=
得到∠ADC=60°，而∠ADC=45°=∠B+∠DAB，根据等腰直角三角形即可求出∠ADC．
解答：在Rt△ADC中
∵=，
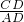∴∠CAD=30°，
∴∠ADC=60°
而∠ADC=∠B+∠DAB
∵△ABC为等腰直角三角形
∴∠B=45°
∴∠DAB=15°．
故选D．
点评：本题利用了：
（1）直角三角形的性质；
（2）三角形的一个外角等于与它不相邻的两个内角和；
（3）等腰直角三角形的性质，两个锐角均为45度．
分析：在Rt△ADC中，由
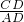=得到∠ADC=60°，而∠ADC=45°=∠B+∠DAB，根据等腰直角三角形即可求出∠ADC．解答：在Rt△ADC中
∵
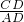=，∴∠CAD=30°，
∴∠ADC=60°
而∠ADC=∠B+∠DAB
∵△ABC为等腰直角三角形
∴∠B=45°
∴∠DAB=15°．
故选D．
点评：本题利用了：
（1）直角三角形的性质；
（2）三角形的一个外角等于与它不相邻的两个内角和；
（3）等腰直角三角形的性质，两个锐角均为45度．
练习册系列答案
相关题目
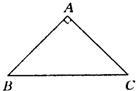32、如图所示，△ABC为等腰直角三角形，斜边BC长为8．
，其中a、b、c为△ABC的三条边，且b≥a，b≥c．
时，这个二次函数取最小值
，证明此时△ABC为正三角形；
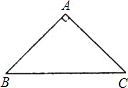如图所示，△ABC为等腰直角三角形，斜边BC长为8．