题目内容
如图1,已知等边△ABC的边长为1,D、E、F分别是AB、BC、AC边上的点(均不与点A、B、C重合),记△DEF的周长为 .
.

(1)若D、E、F分别是AB、BC、AC边上的中点,则 =_______;
=_______;
(2)若D、E、F分别是AB、BC、AC边上任意点,则 的取值范围是 .
的取值范围是 .
小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将 以AC边为轴翻折一次得
以AC边为轴翻折一次得 ,再将
,再将 以
以 为轴翻折一次得
为轴翻折一次得 ,如图2所示. 则由轴对称的性质可知,
,如图2所示. 则由轴对称的性质可知, ,根据两点之间线段最短,可得
,根据两点之间线段最短,可得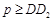 . 老师听了后说:“你的想法很好,但
. 老师听了后说:“你的想法很好,但 的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
 .
.
(1)若D、E、F分别是AB、BC、AC边上的中点,则
 =_______;
=_______;(2)若D、E、F分别是AB、BC、AC边上任意点,则
 的取值范围是 .
的取值范围是 .小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将
 以AC边为轴翻折一次得
以AC边为轴翻折一次得 ,再将
,再将 以
以 为轴翻折一次得
为轴翻折一次得 ,如图2所示. 则由轴对称的性质可知,
,如图2所示. 则由轴对称的性质可知, ,根据两点之间线段最短,可得
,根据两点之间线段最短,可得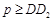 . 老师听了后说:“你的想法很好,但
. 老师听了后说:“你的想法很好,但 的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.解:(1)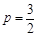 ; ……………………………2分
; ……………………………2分
(2)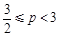 . .……………………………5分
. .……………………………5分
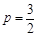 ; ……………………………2分
; ……………………………2分(2)
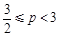 . .……………………………5分
. .……………………………5分分析:(1)根据三角形的中位线的性质即可求得答案;
(2)根据翻折变换的性质将△ABC翻折5次,再利用梯形的性质求解即可.
解:(1)∵等边△ABC的边长为1,
∴AB=AC=BC=1,
∵D、E、F分别是AB、BC、AC边上的中点,
∴DE=
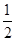 AC=
AC=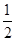 ,EF=
,EF=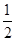 AB=
AB=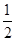 ,DF=
,DF=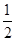 BC=
BC=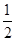 ,
,∴△DEF的周长为p=
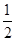 +
+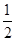 +
+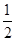 =
=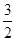 ;
;(2)
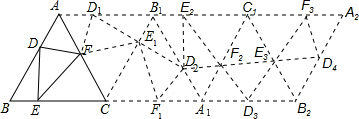
根据题意与由轴对称的性质可知,D2F2+F2E3+E3D4=p,
∵D2与D4分别是A1B1与A2B2的中点时D2、F2、E3、D4共线,
∴当D2与D4分别是A1B1与A2B2的中点时,p最小值为:
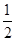 (A1B2+A2B1)=
(A1B2+A2B1)=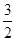 ,
,∵p<AB+AC+BC=3,
∴p的取值范围是:
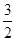 ≤p<3.
≤p<3.故答案为:(1)
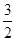 ,(2)
,(2)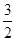 ≤p<3.
≤p<3.
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
 ,则△ABC的周长等于____________
,则△ABC的周长等于____________






 角满足条件:
角满足条件:
