Question

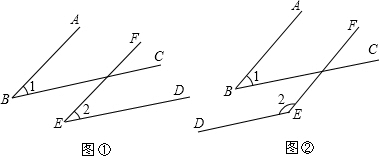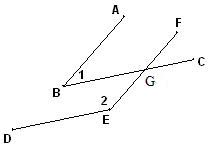
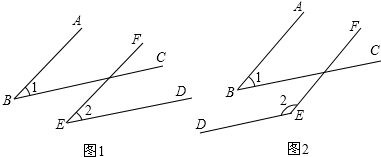
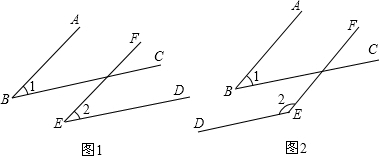
已知一角的两边与另一个角的两边平行，结合图形，试探索这两个角之间的数量关系．
（1）如图①，AB∥EF，BC∥DE，则∠1与∠2的数量关系是

∠1=∠2

．
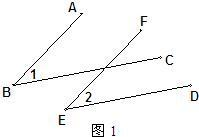
（2）如图②，AB∥EF，BC∥DE，则∠1与∠2的数量关系是

∠1+∠2=180°

．

Answer 1

分析：（1）∠1=∠2，理由为：由AB与EF平行，利用两直线平行同位角相等得到一对角相等，再由BC与ED平行，利用两直线平行同位角相等得到一对角相等，等量代换即可得证；
（2）∠1+∠2=180°，理由为：由AB与EF平行，利用两直线平行同旁内角互补得到一对角互补，再由BC与ED平行，利用两直线平行同位角相等得到一对角相等，等量代换即可得证．

解答：解：（1）∠1=∠2，理由为：
∵AB∥EF，
∴∠1=∠3，
∵BC∥ED，
∴∠3=∠2，
∴∠1=∠2；

（2）∠1+∠2=180°，理由为：
∵AB∥EF，
∴∠1+∠3=180°，
∵BC∥ED，
∴∠3=∠2，
∴∠1+∠2=180°．
故答案为：（1）∠1=∠2；（2）∠1+∠2=180°

点评：此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．