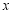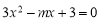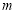题目内容
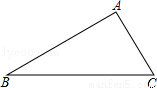
如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为
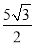 .
.
【解析】
试题分析:此题可以转化为求斜边BC上的高的问题;在Rt△ABC中,∠B=30°,可知∠C=60°;进而在Rt△ADC中,由AC及∠C的正弦值可求得AD的长,即⊙A的半径.
试题解析:过点A作AD⊥BC,
∵∠A=90°,∠B=30°,
∴∠C=60°
∵BC=10,
∴AC= BC=5,
BC=5,
∴AD=AC•sin60°=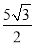 .
.
考点:切线的性质.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
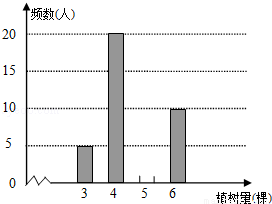
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
植树数量(棵) | 频数(人) | 频率
|
3 | 5 | 0.1 |
4 | 20 | 0.4 |
5 |
|
|
6 | 10 | 0.2 |
合计 | 50 | 1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.