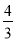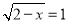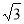题目内容
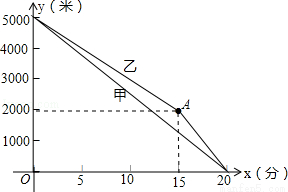
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<x<15的时段内,速度较快的人是 ;
(2)求甲距终点的路程y(米)和跑步时间x(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
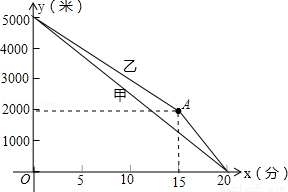
(1) 5000米,甲.(2) y=-250x+5000(0≤x≤20);(3)750米,150米/秒.
【解析】
试题分析:根据图象信息可知,甲运动员图象经过(0,5000)(20,0)所以可用待定系数法求解.距离可根据图象求出,时间可求:20-15=5.速度= 也就迎刃而解了.
也就迎刃而解了.
试题解析:(1)根据图象信息可知他们在进行5000米的长跑训练,直线倾斜程度越大表明变化大;甲.
(2)设所求直线的解析式为:y=kx+b(0≤x≤20),
由图象可知:b=5000,当x=20时,y=0,
∴0=20k+5000,解得k=-250.
即y=-250x+5000(0≤x≤20)
(3)当x=15时,y=-250x+5000=-250×15+5000=5000-3750=1250.
两人相距:(5000-1250)-(5000-2000)=750(米).
两人速度之差: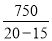 =150(米/分).
=150(米/分).
考点:一次函数的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目