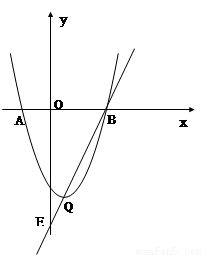题目内容
(本题满分12分 第(1)小题6分,第(2)小题6分)
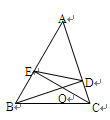
已知:如图,在△ABC中,BD⊥AC于点D, CE⊥AB于点E,EC和BD相交于点O,联接DE.
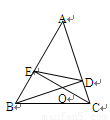
(1)求证:△EOD∽△BOC;
(2)若S△EOD=16,S△BOC=36,求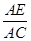 的值.
的值.
(1)首先根据已知条件证得△BOE∽△COD,从而得出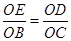
再加上对顶角相等的条件即可得证所求。
(2)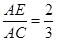
【解析】
试题分析:(1)证明:在△BOE与△DOC中

∵∠BEO=∠CDO,∠BOE=∠COD
∴△BOE∽△COD………………………………………(2分)
∴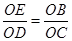 ……………………………………………(1分)
……………………………………………(1分)
即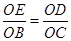 ……………………………………………(1分)
……………………………………………(1分)
又∵∠EOD=∠BOC……………………………………(1分)
∴△EOD∽△BOC………………………………………(1分)
(2) ∵△EOD∽△BOC
∴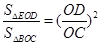 ………………………………………………………………(1分)
………………………………………………………………(1分)
∵S△EOD=16,S△BOC=36
∴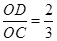 ………………………………………………………………………(1分)
………………………………………………………………………(1分)
在△ODC与△EAC中
∵∠AEC=∠ODC,∠OCD=∠ACE
∴△ODC∽△AEC………………………………………………………………(1分)
∴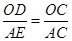 ……………………………………………………………………(1分)
……………………………………………………………………(1分)
即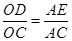 ……………………………………………………………………(1分)
……………………………………………………………………(1分)
∴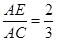 ………………………………………………………………………(1分)
………………………………………………………………………(1分)
考点:相似三角形
点评:三角形相似的性质与判定是相对应的,首先(1)中利用两边对应成比例且夹角相等,两个三角形相似证得相似,然后(2)中即可利用所求结论进行新的问题求解条件,这是很多综合题的共性。有时即使第一问无法证明,在计算后续问题时也可使用该条件,这是学生解题时的一个小技巧。



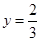 x2
x2 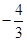 x
x 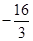 的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.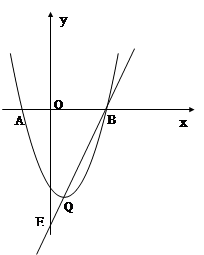
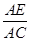 的值.
的值.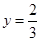 x2
x2
 x
x 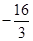 的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.