题目内容
（本题满分12分，第(1)小题4分，第(2)小题4分、第(3)小题4分）
如图8，在平面直角坐标系xOy中，半径为
的
与x轴交于
、
两点，且点C在x轴的上方．
（1）求圆心C的坐标；
（2）已知一个二次函数的图像经过点
、B、C，求这二次函数的解析式；
（3）设点P在y轴上，点M在（2）的二次函数图像上，如果以点P、M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标.
解：（1） 联结AC，过点C作
，垂直为H，
由垂径定理得：AH=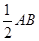
＝2，…………………………………（1分）
则OH＝1．…………………………………………………………（1分）
由勾股定理得：CH＝4．…………………………………………（1分）
又点C在x轴的上方，∴点C的坐标为
．………………（1分）
（2）设二次函数的解析式为
由题意，得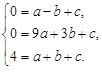
解这个方程组，得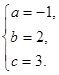
………………………………………（3分）
∴ 这二次函数的解析式为y =－x2+2x＋3．………………………………（1分）
（3）点M的坐标为
…………………………………………………（2分）
或
或
……………………………（2分）
解析:略
练习册系列答案
计算高手系列答案
相关题目
的
与x轴交于
、
两点，且点C在x轴的上方．
、B、C，求这二次函数的解析式；
的
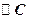与x轴交于
、
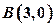两点，且点C在x轴的上方．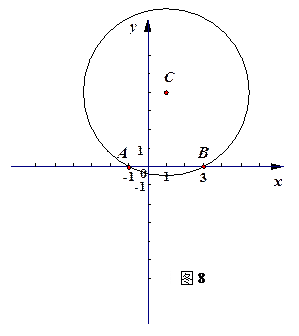
、B、C，求这二次函数的解析式；
M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标.
=
，求证：
．
足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．
，求证：四边形OCBD是菱形．
轴相交于点F，点Q为直线AD上一点，且△ABQ与△ADF相似，直接写出点Q点的坐标．