ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþµƒ∂‘≥∆÷· «y÷·£¨«“µ„£®2£¨2£©£¨£®1£¨ ![]() £©‘⁄≈◊ŒÔœþ…œ£¨µ„P «≈◊ŒÔœþ…œ≤ª”Î∂•µ„N÷ÿ∫œµƒ“ª∂ص„£¨π˝P◊˜PA°Õx÷·”⁄A£¨PC°Õy÷·”⁄C£¨—”≥§PCΩª≈◊ŒÔœþ”⁄E£¨…ËM «Oπÿ”⁄≈◊ŒÔœþ∂•µ„Nµƒ∂‘≥∆µ„£¨D «Cµ„πÿ”⁄Nµƒ∂‘≥∆µ„£Æ
£©‘⁄≈◊ŒÔœþ…œ£¨µ„P «≈◊ŒÔœþ…œ≤ª”Î∂•µ„N÷ÿ∫œµƒ“ª∂ص„£¨π˝P◊˜PA°Õx÷·”⁄A£¨PC°Õy÷·”⁄C£¨—”≥§PCΩª≈◊ŒÔœþ”⁄E£¨…ËM «Oπÿ”⁄≈◊ŒÔœþ∂•µ„Nµƒ∂‘≥∆µ„£¨D «Cµ„πÿ”⁄Nµƒ∂‘≥∆µ„£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞∂•µ„Nµƒ◊¯±Í£ª
£®2£©«Û÷§£∫Àƒ±þ–ŒPMDA «∆Ω––Àƒ±þ–Œ£ª
£®3£©«Û÷§£∫°˜DPE°◊°˜PAM£¨≤¢«Û≥ˆµ±À¸√«µƒœýÀ∆±»Œ™ ![]() ±µƒµ„Pµƒ◊¯±Í£Æ
±µƒµ„Pµƒ◊¯±Í£Æ
°æ¥∞∏°ø
£®1£©
Ω‚£∫°þ≈◊ŒÔœþµƒ∂‘≥∆÷· «y÷·£¨
°ýø……Ë≈◊ŒÔœþΩ‚Œˆ ΩŒ™y=ax2+c£¨
°þµ„£®2£¨2£©£¨£®1£¨ ![]() £©‘⁄≈◊ŒÔœþ…œ£¨
£©‘⁄≈◊ŒÔœþ…œ£¨
°ý 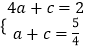 £¨Ω‚µ√
£¨Ω‚µ√ ![]() £¨
£¨
°ý≈◊ŒÔœþΩ‚Œˆ ΩŒ™y= ![]() x2+1£¨
x2+1£¨
°ýNµ„◊¯±ÍŒ™£®0£¨1£©
£®2£©
÷§√˜£∫…ËP£®t£¨ ![]() t2+1£©£¨‘ÚC£®0£¨
t2+1£©£¨‘ÚC£®0£¨ ![]() t2+1£©£¨PA=
t2+1£©£¨PA= ![]() t2+1£¨
t2+1£¨
°þM «Oπÿ”⁄≈◊ŒÔœþ∂•µ„Nµƒ∂‘≥∆µ„£¨D «Cµ„πÿ”⁄Nµƒ∂‘≥∆µ„£¨«“N£®0£¨1£©£¨
°ýM£®0£¨2£©£¨
°þOC= ![]() t2+1£¨ON=1£¨
t2+1£¨ON=1£¨
°ýDM=CN= ![]() t2+1©Å1=
t2+1©Å1= ![]() t2£¨
t2£¨
°ýOD= ![]() t2©Å1£¨
t2©Å1£¨
°ýD£®0£¨©Å ![]() t2+1£©£¨
t2+1£©£¨
°ýDM=2©Å£®©Å ![]() t2+1£©=
t2+1£©= ![]() t2+1=PA£¨«“PM°ŒDM£¨
t2+1=PA£¨«“PM°ŒDM£¨
°ýÀƒ±þ–ŒPMDAŒ™∆Ω––Àƒ±þ–Œ
£®3£©
Ω‚£∫Õ¨£®2£©…ËP£®t£¨ ![]() t2+1£©£¨‘ÚC£®0£¨
t2+1£©£¨‘ÚC£®0£¨ ![]() t2+1£©£¨PA=
t2+1£©£¨PA= ![]() t2+1£¨PC=|t|£¨
t2+1£¨PC=|t|£¨
°þM£®0£¨2£©£¨
°ýCM= ![]() t2+1©Å2=
t2+1©Å2= ![]() t2©Å1£¨
t2©Å1£¨
‘⁄Rt°˜PMC÷–£¨”…π¥π…∂®¿Ìø…µ√PM= ![]() =
= ![]() =
= ![]() =
= ![]() t2+1=PA£¨«“Àƒ±þ–ŒPMDAŒ™∆Ω––Àƒ±þ–Œ£¨
t2+1=PA£¨«“Àƒ±þ–ŒPMDAŒ™∆Ω––Àƒ±þ–Œ£¨
°ýÀƒ±þ–ŒPMDAŒ™¡‚–Œ£¨
°ý°œAPM=°œADM=2°œPDM£¨
°þPE°Õy÷·£¨«“≈◊ŒÔœþ∂‘≥∆÷·Œ™y÷·£¨
°ýDP=DE£¨«“°œPDE=2°œPDM£¨
°ý°œPDE=°œAPM£¨«“ ![]() =
= ![]() £¨
£¨
°ý°˜DPE°◊°˜PAM£ª
°þOA=|t|£¨OM=2£¨
°ýAM= ![]() £¨«“PE=2PC=2|t|£¨
£¨«“PE=2PC=2|t|£¨
µ±œýÀ∆±»Œ™ ![]() ±£¨‘Ú
±£¨‘Ú ![]() =
= ![]() £¨º¥
£¨º¥ ![]() =
= ![]() £¨Ω‚µ√t=2
£¨Ω‚µ√t=2 ![]() ªÚt=©Å2
ªÚt=©Å2 ![]() £¨
£¨
°ýPµ„◊¯±ÍŒ™£®2 ![]() £¨4£©ªÚ£®©Å2
£¨4£©ªÚ£®©Å2 ![]() £¨4£©
£¨4£©
°æΩ‚Œˆ°ø£®1£©”…“—÷™µ„µƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«Ûµ√≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨ø…«Ûµ√∆‰∂•µ„Nµƒ◊¯±Í£ª£®2£©…ËPµ„∫·◊¯±ÍŒ™t£¨‘Úø…±Ì æ≥ˆC°¢D°¢M°¢Aµƒ◊¯±Í£¨¥”∂¯ø…±Ì æ≥ˆPA∫ÕDMµƒ≥§£¨”…PA=DMø…÷§µ√Ω·¬€£ª£®3£©…ËPµ„∫·◊¯±ÍŒ™t£¨‘⁄Rt°˜PCM÷–£¨ø…±Ì æ≥ˆPM£¨ø…«Ûµ√PM=PA£¨ø…÷™Àƒ±þ–ŒPMDAŒ™¡‚–Œ£¨”…¡‚–Œµƒ–‘÷ ∫Õ≈◊ŒÔœþµƒ∂‘≥∆–‘ø…µ√°œPDE=°œAPM£¨ø…÷§µ√Ω·¬€£¨‘⁄Rt°˜AOM÷–£¨”√t±Ì æ≥ˆAMµƒ≥§£¨‘Ÿ±Ì æ≥ˆPEµƒ≥§£¨”…œýÀ∆±»Œ™ ![]() ø…µ√µΩπÿ”⁄tµƒ∑Ω≥ã¨ø…«Ûµ√tµƒ÷µ£¨ø…«Ûµ√Pµ„◊¯±Í£Æ
ø…µ√µΩπÿ”⁄tµƒ∑Ω≥ã¨ø…«Ûµ√tµƒ÷µ£¨ø…«Ûµ√Pµ„◊¯±Í£Æ
°æøºµ„æ´Œˆ°ø∏˘æðƒøµƒ“—÷™Ãıº˛£¨¿˚”√¡‚–Œµƒ–‘÷ µƒœýπÿ÷™ ∂ø…“‘µ√µΩŒ µƒ¥∞∏£¨–Ë“™’∆Œ’¡‚–ŒµƒÀƒÃı±þ∂ºœýµ»£ª¡‚–Œµƒ∂‘Ω«œþª•œý¥π÷±£¨≤¢«“√ø“ªÃı∂‘Ω«œþ∆Ω∑÷“ª◊È∂‘Ω«£ª¡‚–Œ±ª¡ΩÃı∂‘Ω«œþ∑÷≥…Àƒ∏ˆ»´µ»µƒ÷±Ω«»˝Ω«–Œ£ª¡‚–Œµƒ√ʪ˝µ»”⁄¡ΩÃı∂‘Ω«œþ≥§µƒª˝µƒ“ª∞ΣÆ

°æƒø°øƒ≥–£æˆ∂®º”«ø”√´«Ú°¢¿∫«Ú°¢∆π≈“«Ú°¢≈≈«Ú°¢◊„«ÚŒÂœÓ«Ú¿ý‘À∂Ø£¨√øŒªÕ¨—ß±ÿ–Ϋ“÷ªƒÐ—°‘Ò“ªœÓ«Ú¿ý‘À∂Ø£¨∂‘∏√–£—ß…˙Àʪ˙≥È»°10%Ω¯––µ˜≤È£¨∏˘æðµ˜≤ÈΩ·π˚ªÊ÷∆¡À»Áœ¬≤ªÕÍ’˚µƒ∆µ ˝∑÷≤º±Ì∫Õ…»–ŒÕ≥º∆Õº£∫
‘À∂؜Ӄø | ∆µ ˝£®»À ˝£© |
”√´«Ú | 30 |
¿∫«Ú | a |
∆π≈“«Ú | 36 |
≈≈«Ú | b |
◊„«Ú | 12 |

«Î∏˘æð“‘…œÕº±Ì–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®1£©∆µ ˝∑÷≤º±Ì÷–µƒa= £¨ b=£ª
£®2£©‘⁄…»–ŒÕ≥º∆Õº÷–£¨°∞≈≈«Ú°±À˘‘⁄µƒ…»–Œµƒ‘≤–ƒΩ«Œ™∂»£ª
£®3£©»´–£”–∂ý…Ÿ√˚—ß…˙—°‘Ò≤Œº”∆π≈“«Ú‘À∂Ø£ø






