��Ŀ����
����Ŀ����֪����ͼ���ı���ABCD�У�˳����������е�E��F��G��H�õ����ı���EFGH�����ı���ABCD���е��ı��Σ�
��1���ı���EFGH����״��______��֤����Ľ��ۣ�
��2������̽����ͬ�ı��ε��е��ı��ε���״��
�ٵ��ı���ABCD��Ϊƽ���ı���ʱ�������е��ı�����______��
�ڵ��ı���ABCD��Ϊ����ʱ�������е��ı�����______��
�۵��ı���ABCD��Ϊ����ʱ�������е��ı�����______��
�ܵ��ı���ABCD��Ϊ������ʱ�������е��ı�����______��
��3���������Ϲ۲�̽���������ܽ��е��ı��ε���״����ԭ�ı��ε�ʲô���ʾ����ģ�
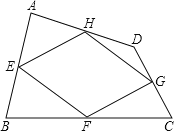
���𰸡���1���ı���EFGH��ƽ���ı��Σ�����������2����ƽ���ı��Σ������Σ��۾��Σ��������Σ�
��������
(1)����BD��������������λ�߶����Ƴ������ı��ζԱ�ƽ������ȣ���Ϊƽ���ı��Σ�
(2)Ӧ����������λ�߶����������ε���λ�ߵ��ڵ����ߵ�һ����������ƽ���ı��ε��ж������ε��ж������ε��ж��������ε��ж�����⼴�ɣ�
(3)�����Ϸ����֪���е��ı��ε���״����ԭ�ı��εĶԽ��ߵĴ�С��ϵ��λ�ù�ϵ�����ģ�
(1)�ı���EFGH��ƽ���ı��Σ�֤�����£�
��ͼ1������BD��
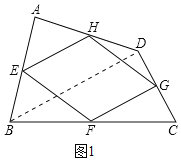
��E��H�ֱ���AB��AD���е㣬
��EH����ABD����λ�ߣ�
��EH=![]() BD��EH��BD��
BD��EH��BD��
ͬ����FG=![]() BD��FG��BD��
BD��FG��BD��
��EH=FG��EH��FG��
���ı���EFGH��ƽ���ı��Σ�
�ʴ�Ϊ��ƽ���ı��Σ�
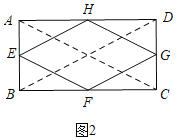
(2)��ͬ���ã����ı���ABCD��Ϊƽ���ı���ʱ�������е��ı����ǣ�ƽ���ı��Σ�
����ͼ2������AC��BD��
���ı���ABCD�Ǿ��Σ�
��AC=BD��
��EF=![]() AC��EH=
AC��EH=![]() BD��
BD��
��EF=EH��
���ı���EFGH�����Σ�
�ۡ��ı���EFGH�����Σ�
��AC��BD��
���FEH=90����
���ı���ABCD�Ǿ��Σ�
�ܡ��ı���ABCD�������Σ�
��AC=BD��AC��BD��
���ı���EFGH�������Σ�
(3)�����Ϸ����֪���е��ı��ε���״����ԭ�ı��εĶԽ��ߵĴ�С��ϵ��λ�ù�ϵ�����ģ�