题目内容
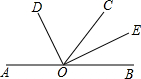 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
分析:(1)OD平分∠AOC,OE平分∠BOC,得出∠DOE=
(∠BOC+∠COA),代入数据求得问题;
(2)利用(1)的结论,把∠BOC=a°,代入数据求得问题;
(3)根据(1)(2)找出互余的角即可.
| 1 |
| 2 |
(2)利用(1)的结论,把∠BOC=a°,代入数据求得问题;
(3)根据(1)(2)找出互余的角即可.
解答:解:(1)∵OD平分∠AOC,OE平分∠BOC,
∴∠DOC=
∠AOC,∠COE=
∠BOC
∴∠DOE=∠DOC+∠COE=
(∠BOC+∠COA)=
×(62°+180°-62°)=90°;
(2)∠DOE═
(∠BOC+∠COA)=
×(a°+180°-a°)=90°;
(3)∠DOA与∠COE互余;∠DOA与∠BOE互余;∠DOC与∠COE互余;∠DOC与∠BOE互余.
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠DOC+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∠DOE═
| 1 |
| 2 |
| 1 |
| 2 |
(3)∠DOA与∠COE互余;∠DOA与∠BOE互余;∠DOC与∠COE互余;∠DOC与∠BOE互余.
点评:此题考查角平分线的意义以及余角的意义.

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=